ABCDEF is a regular hexagon. Show that :
−−→OA+−−→OB+−−→OC+−−→OD+−−→OE+−−→OF=→0
Step by step video & image solution for ABCDEF is a regular hexagon. Show that : vec(OA)+vec(OB)+vec(OC)+vec(OD)+vec(OE)+vec(OF)=vec(0) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR ALGEBRA BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - EXERCISE 10 (c ) Short Answer Type Questions
39 Videos
- VECTOR ALGEBRA BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - EXERCISE 10 (c ) Long Answer Type Questions (I)
12 Videos
- VECTOR ALGEBRA BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - EXERCISE 10 (a) Short Answer Type Questions
21 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - MODERN PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - CHAPTER TEST 11
11 Videos
Similar Questions
Knowledge Check
If ABCDEF is a regular hexagon , then A→D+E→B+F→C equals
A2A→BB→0C3A→BD4A→BABCDEF is a regular hexagon with point O as centre. The value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF is
A2−−→AOB2−−→AOC6−−→AOD0
In a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
View SolutionLet O be the centre of the regular hexagon ABCDEF then find −−→OA+−−→OB+−−→OD+−−→OC+−−→OE+−−→OF
View SolutionABCDEF is a regular hexagon with centre a the origin such that −−→AB+−−→EB+−−→FC=λ−−→ED then λ= (A) 2 (B) 4 (C) 6 (D) 3
View SolutionIf O(→0) is the circumcentre and O' the orthocentre of a triangle ABC, then prove that
i. −−→OA+−−→OB+−−→OC=−−−→OO'
ii. −−−→O'A+−−−→O'B+−−−→O'C=2−−−→O'O
iii. −−−→AO'+−−−→O'B+−−−→O'C=2−−→AO=−−→AP
where AP is the diameter through A of the circumcircle.
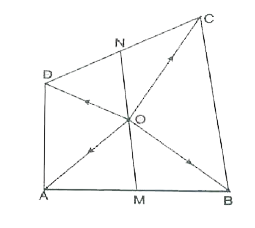
View SolutionIn the figure, M is the mid - point of [AB] and N is the mid - point of [CD] and O is the mid - point of [MN]. Prove that :
(i) −−→OA+−−→OB+−−→OC+−−→OD=→0
(ii) −−→BC+−−→AD=2−−−→MN.
View SolutionABCD is a quadrilateral and E is the point of intersection of the lines joining the middle points of opposite side. Show that the resultant of −−→OA , −−→OB , −−→OC and −−→OD = 4 −−→OE , where O is any point.
View Solution
