If y=x for x>0,y=0, for x=0,y=−x,x<0, then at x=0, y is :
not continuous
differentiable
continuous but not differentiable
None of these.
The correct Answer is:C
Topper's Solved these Questions
- DIFFERENTIABILITY AND DIFFERENTIATION BOOK - MODERN PUBLICATIONCHAPTER - DIFFERENTIABILITY AND DIFFERENTIATION EXERCISE - MCQs (LEVEL-II)
35 Videos
- DIFFERENTIABILITY AND DIFFERENTIATION BOOK - MODERN PUBLICATIONCHAPTER - DIFFERENTIABILITY AND DIFFERENTIATION EXERCISE - Latest Question from AIEEE/JEE Examinations
7 Videos
- DETERMINANTS BOOK - MODERN PUBLICATIONCHAPTER - DETERMINANTS EXERCISE - Recent competitive Questions
10 Videos
- DIFFERENTIAL EQUATIONSBOOK - MODERN PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Recent competitive Questions
12 Videos
Similar Questions
Knowledge Check
If x>0andxy=1, the minimum value of (x+y) is
A1B0C2D√2Let f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩tan2[x]x2−[x]21√|x|cot|x|forx>0forx=0forx<0where[x] and {x} denote respectively the greatest integer less than equal to x and the fractional part of x, then
Alimx→0+f(x)=1Blimx→0−f(x)=1Ccot−1{limx→0−f(x)}2=π4DAll of theseIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x−1,x<014,x=0x2,x>0 , then
Alimx→0+f(x)=1Blimx→0−f(x)=1Cf (X) is discontinuous at x = 0DNone of these
Let f(x) be a function which satisfy the equation f(xy)=f(x)+f(y) for all x>0,y>0 such that f'(1)=2. Find the area of the region bounded by the curves y=f(x),y=∣∣x3−6x2+11x−6∣∣andx=0.
View SolutionShow that the Signum Function f:R→R, given by :
f(x)=⎧⎪⎨⎪⎩1, if x>00, if x=0-1, if x<0 is neither one-one nor onto.
View SolutionState which of the following statements is true of false.
(i) If x<yandb<0, then xb<yb.
(ii) If xy>0, then x>0andy<0
(iii) If xy>0, then x<0andy<0
(iv) If xy<0, then x<0andy<0
(v) If x<−5andx<−2, than x∈(−∞,−5)
(vi) If x<−5andx>2, then x∈(−5,2)
(vii) If x>−2andx<9,then x∈(−2,9)
(viii) If |x|>5, then x∈(−∞,−5)∪[5,∞)
(ix) If |x|≤4, then x∈[−4,4]
(x)Graph of x<3is
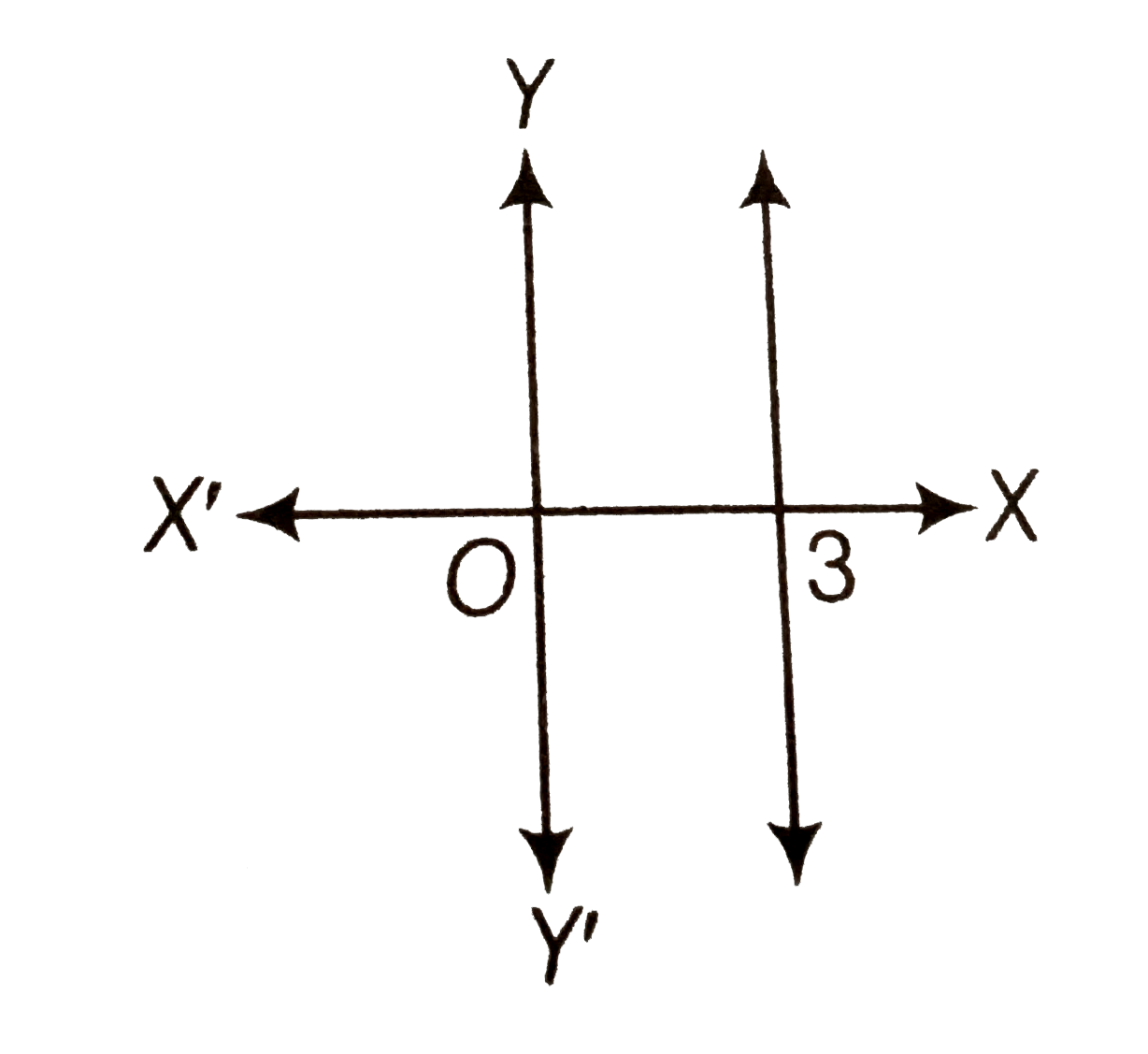
(xi) Graph of x≥0 is

(xii) Graph of y≤0 is
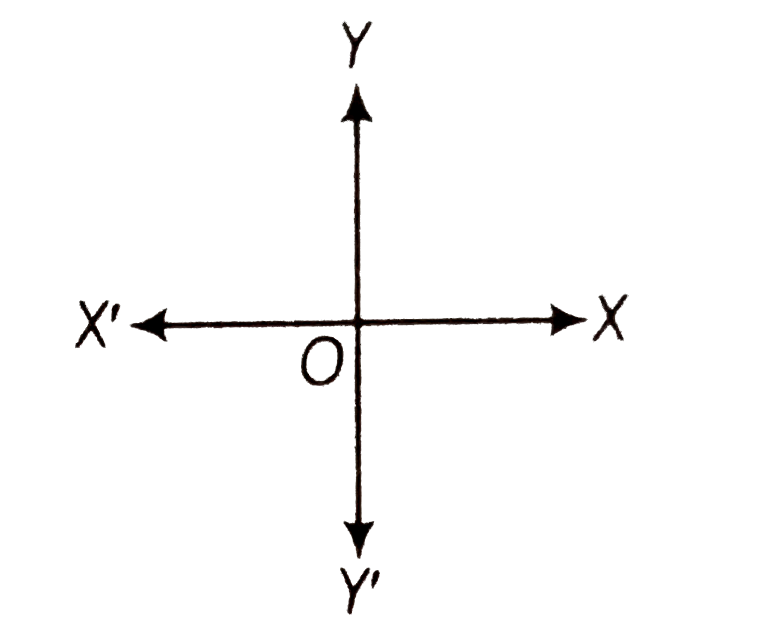
(xiii) Solution set of x≤0andy≤0 is

(xiv) Solution set of x≥0andy≤1 is
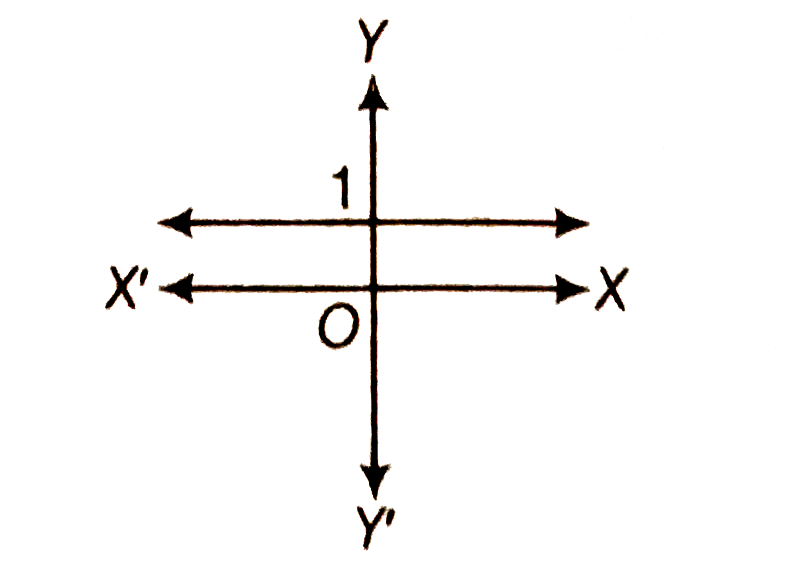
(xv) Solution set of x+y≥0 is
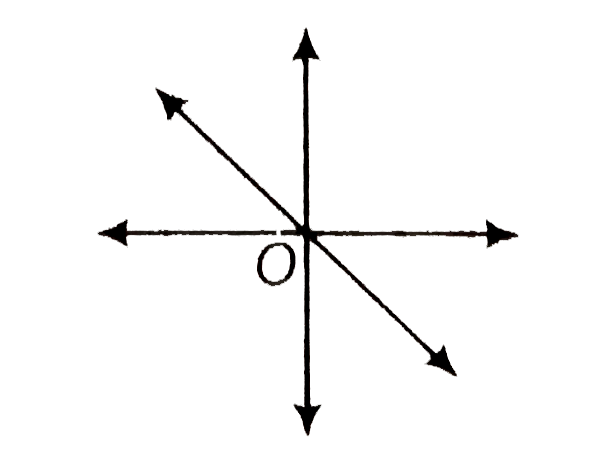
View SolutionDraw the graph of the function
f(x)=⎧⎪⎨⎪⎩1 if x>00 if x=0-1 if x<0,x∈R
View SolutionIf f(x)=⎧⎪⎨⎪⎩|x|+1x<00x=0|x|−1x>0
for what value (s) of a does limx→af(x) exists?
View Solution
