An equivalence relation R in A divides it into equivalence classesA1,A2,A3What is the value ofA1∪A2∪A3andA1∩A2∩A3
The correct Answer is:=ϕ
To solve the question regarding the equivalence classes A1,A2, and A3 formed by the equivalence relation R in set A, we will analyze the properties of equivalence classes and their unions and intersections.
1. Understanding Equivalence Classes:
- An equivalence relation on a set A partitions A into disjoint subsets known as equivalence classes. Each element of A belongs to exactly one equivalence class.
2. Identify the Union of Equivalence Classes:
- The union of the equivalence classes A1,A2, and A3 is represented as:
A1∪A2∪A3
- Since these classes are disjoint and cover the entire set A, the union of all equivalence classes will equal the original set A:
A1∪A2∪A3=A
3. Identify the Intersection of Equivalence Classes:
- The intersection of the equivalence classes A1,A2, and A3 is represented as:
A1∩A2∩A3
- Since the equivalence classes are disjoint, they do not share any elements. Therefore, the intersection of any two or more disjoint sets is the empty set:
A1∩A2∩A3=∅
Final Answers:
- The value of A1∪A2∪A3 is A.
- The value of A1∩A2∩A3 is ∅.
- An equivalence relation on a set A partitions A into disjoint subsets known as equivalence classes. Each element of A belongs to exactly one equivalence class.
- The union of the equivalence classes A1,A2, and A3 is represented as:
A1∪A2∪A3
- Since these classes are disjoint and cover the entire set A, the union of all equivalence classes will equal the original set A:
A1∪A2∪A3=A
- The intersection of the equivalence classes A1,A2, and A3 is represented as:
A1∩A2∩A3
- Since the equivalence classes are disjoint, they do not share any elements. Therefore, the intersection of any two or more disjoint sets is the empty set:
A1∩A2∩A3=∅
- The value of A1∪A2∪A3 is A.
- The value of A1∩A2∩A3 is ∅.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The number of all triplets (a1,a2,a3) such that a1+a2cos2x+a3sin2x=0 for all x is : (A) 0 (B) 1 (C) 3 (D) Infinite
AzeroBoneCthreeDinfiniteIf a1,a2 and a3 are three numbers satisfying a21+a22+a23=1 , then the maximum value of
(4a1−3a2)2+(5a2−4a3)2+(3a3−5a1)2 is k, then [k14] is equal to (where [.] denotes the greatest integer function )A1B2C3D4Three distinct numbers a1,a2,a3 are in increasing G.P. a21+a22+a23=364and a1+a2+a3=26 then the value of a10 if an is the nth term of the given G.P. is:
A2.39B39C2.310D312
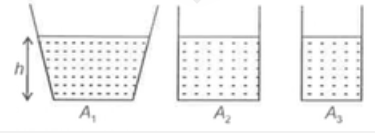
Three vessels containing same liquid, upto the same height h, then pressure at the bottom is (A1>A2>A3)
View SolutionFor a post three person A1,A2,A3 appear in the interview. The probability of A1 being selected is twice as much as that of A2 and the probability of A2 being selected is three times as much as that of A3. What are the individual probabilities of A1,A2,A3 being selected?
View SolutionThree rectangles A1, A2 and A3 have the same area. Their lengths a1, a2 and a3 respectively are such that a1<a2<a3 . Cylinders C1, C2 and C3 are formed from A1, A2 and A3 respectively by joining the parallel sides along the breadth. Then C1 will enclosed maximum volume (b) C2 will enclosed maximum volume (c) C3 will enclosed maximum volume (d) Each of C1, C2 and C3 will enclose equal volume
View SolutionFor any three sets A1,A2,A3. Let B1=A1,B2=A2−A1andB3=A3−A1∪A2 , then which of the following statement is always true ?
View SolutionThe equation Ax−a1+A2x−a2+A3x−a3=0whereA1,A2,A3>0anda1<a2<a3 has two real roots lying in the invervals. (A) (a1,a2)and(a2,a3) (B) (−∞,a1)and(a3,∞) (C) (A1,A3)and(A2,A3) (D) none of these
View Solution
