चित्र में बिंदु A पर PQ एक स्पर्श रेखा और PBC एक छेदक रेखा है। यदि AD कोण BAC का समद्विभाजक हो, तो सिद्ध कीजिये क़ि एक त्रिभुज ADP समद्विबाहु त्रिभुज है।
The correct Answer is:△ADP समद्विभाहु त्रिभुज है
Topper's Solved these Questions
- वृत्त एवं स्पर्श रेखा BOOK - TRIPUTI PUBLICATIONCHAPTER - वृत्त एवं स्पर्श रेखा EXERCISE - अतिलघुतरात्मक निबंधात्मक प्रश्न
8 Videos
- वास्तविक संख्या BOOK - TRIPUTI PUBLICATIONCHAPTER - वास्तविक संख्या EXERCISE - लघुरात्मक एव निबन्धात्मक प्रश्न
9 Videos
- वृत्त की परिधि एवं क्षेत्रफल BOOK - TRIPUTI PUBLICATIONCHAPTER - वृत्त की परिधि एवं क्षेत्रफल EXERCISE - अतिलघुतरात्मक एवं निबंधात्मक प्रशन
9 Videos
Similar Questions
सिद्ध कीजिए क़ि किसी बाह्य बिंदु से किसी वृत्त पर खींची गयी स्पर्श रेखाओ के बीच का कोण स्पर्श बिन्दुओ को मिलाने वाले रेखाखण्ड द्वारा केंद्र पर अंतरित कोण का समपूरक होता है।
View Solutionसिद्ध कीजिए कि √3 एक परिमेय संख्या है।
View Solutionएक वृत्त का चाप केंद्र पर 60∘ का कोण अंतरित करता है। यदि इसके लघुत्रिज्यखंड का क्षेत्रफल 231 सेमी ^(2) है ,तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
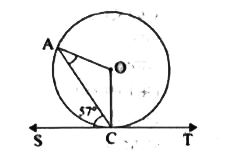
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionदिये गये चित्र में स्पर्श रेखा है -

View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
View Solutionदिये गये चित्र में स्पर्श रेखा है:

View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात किजिए जिसके शीर्ष बिंदु A(1,1,1),B(1,2,3) और C(2,3,4) है।
View Solutionवृत्त x2+y2=4 के बिंदु (√3,1) पर खींची गई स्पर्श रेखा और अभिलम्ब तथा X-अक्ष एक त्रिभुज बनाते है । इस त्रिभुज का (वर्ग इकाइयो में) क्षेत्रफल है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solution
