A uniform thin .................
The correct Answer is:4
Force on element dx on rod (taken at distance x from centre of earth) is
df=(mRdx)GMx2
Total force on rod is
F=∫df=GMmR2R∫R1x2dx
=GMmR[−1x]2RR
=GMm2R2
Topper's Solved these Questions
- TEST PAPERBOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY
37 Videos
- TEST PAPERBOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY
37 Videos
- SEQUENCE & SERIES BOOK - RESONANCECHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)
3 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
263 Videos
Similar Questions
A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View Solution
Knowledge Check
A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
AL/2B2L/3CL/4DL/5Find out the position vector of centre of mass of the trapezium made out of uniform thin rods of same material.
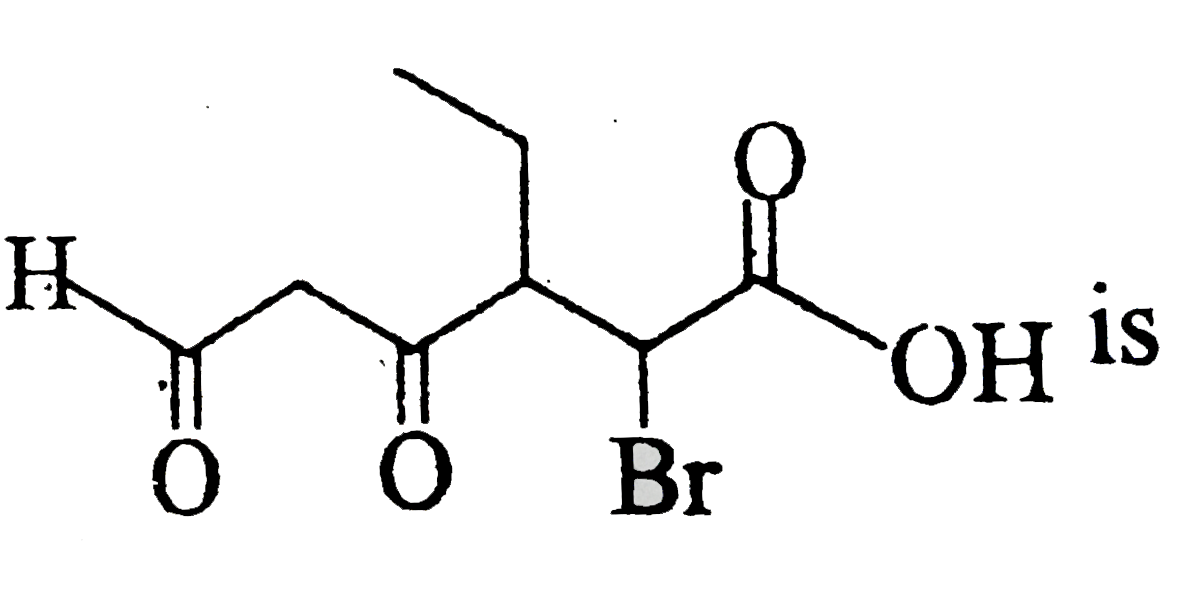 A(√2+11)ˆi−(√2+3)ˆj√2+4B(√2+3)ˆi+(√2+11)ˆj√2+4C(√2+11)ˆi+(√2+3)ˆj√2+4D2ˆi+ˆj
A(√2+11)ˆi−(√2+3)ˆj√2+4B(√2+3)ˆi+(√2+11)ˆj√2+4C(√2+11)ˆi+(√2+3)ˆj√2+4D2ˆi+ˆjIf gravitational field due to uniform thin hemispherical shell at point P is I, then the magnitude of gravitational field at Q is (Mass of hemispherical shell is M, radius is R)
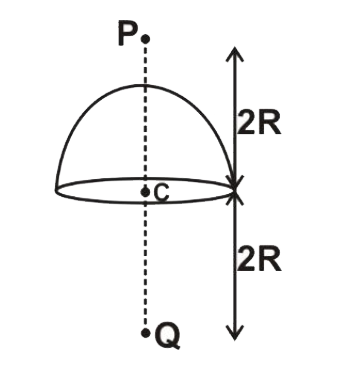 AGM2R2−IBGM2R2+ICGM4R−ID2I−GM2R2
AGM2R2−IBGM2R2+ICGM4R−ID2I−GM2R2
If gravitational field due to uniform thin hemispherical shell at point P is I, then the magnitude of gravitational field at Q is (Mass of hemispherical shell is M, radius is R)

View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionFour identical uniform thin rods, each of mass m and length l are joined to a common point O as shown in the figure. Moment of inertia of the system about an axis passing through O and lying in the plane of rods is
View SolutionThree uniform thin rods, each of mass 1 kg and length √3\ m, are placed along three co-ordinate axes with one end at the origin. The moment of inertia of the system about X-axis is
View SolutionTwo uniform thin rods each of mass M and length I are placed along X and Y-axis with one end of each at the origin. M.I. of the system about Z-axis is
View Solution
