To find the distance d over which a signal can be seen clearly in foggy conditions, a railways engineer uses dimensional analysis and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. The engineer finds that d is proportional to S1/n. The value of n is.
Density : [p]=[MLT−3]
Intensity : [S]=[ML2T−3L2]=[MT−3]
Frequency : [f]=[T−1]
Let us assume that
d∝paSbfc
⇒[d]=[p]a[S]b[f]c
imlplies[L]=[ML−3]a[MT−3]b[T−1]c
⇒[L]=[Ma+bL−3aT−3b−c]
On comparing dimensions on both the sides we get the following :
−3a=1⇒a=−1/3
a+b=0⇒b=−a=1/3
We can see that d∝S13
Hence value of n =3.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST15videos
UNITS AND MEASUREMENT
- BOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS)1videos
UNITS AND MEASUREMENT
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
WAVES
Similar Questions
To find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View Solution[" A solid sphere of radius "R" is charged with "],[" volume charge density "rho=Kr^(n)," where "K" and "n],[" are constants and "r" is the distance from its "],[" centre.If electric field inside the sphere at "],[" distance "r" is proportional to "r^(4)," then find the "],[" value of "n.]
View Solution
Knowledge Check
- Question 1 - Select One
In Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Distance d between S1andS2 is
A0.2 mmB45μmC20μmDnone of these - Question 2 - Select One
In Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. When the screen is at position (2), its distance from the double slits is nearly
A30 cmB20 cmC38 cmDnone of these
A satellite S1 of mass m is revolving at a distance of R from centre of earth and the other satellite S2 of mass 4m is revolving at a distance of 4R from the centre of earth. The time periods of revolution of two satellites are in the raito 1 : n. Find the value of n.
View SolutionAssume that the de Brogie wave associated with an electron can can from a standing wave between the atome arrange in a one dimensional array with nodes at each of the atomic sites it is found that one such standing wave if the distance d between the aloms of the arry is 2M139waveisaga∈formadifdis∈creased→2.5Å . A similar standing in the distance if d find the energy of the electrons velts and tghe least value of d for which the standing wave type described above can from .
View SolutionA block of mass 3kg is attached with an ideal spring of spring constant 900 N/m. The other end of the spring connected with a rigid wall. A fixed convex mirror of radius of curvature 120 cm is placed at a distance 110 cm from the block and the spring is in its natural length. the spring is extended by 100 cm and released. the speed of the image of block is (15n)ms, when extension in the spring remains 50 cm. Find the value of 'n'.
View SolutionMonochromatic light of wavelength λ passes through a very narrow slit S and then strikes a screen placed at a distance D = 1m in which there are two parallel slits S1 and S2 as shown. Slit S1 is directly in line with S while S2 is displaced a distance d to one side. The light is detected at point P on a second screen, equidistant from S1 and S2 When either slit S1 or S2 is open equal light intensities I are measured at point P. When both slits are open, the intensity is three times as large i.e. 3I. If the minimum possible wavelength is Nd2, then find the value of N(d<<D)
View SolutionIn a Young's double slit experiment, slits are seperated by a distance d and screen is at distance D, (D>>d) from slit plane. If light source of wavelength λ(λ<<d) is used. The minimum distance from central point on the screen where intensity is one fourth of the maximum is Dλnd. Find the value of n.
View SolutionA point source of light, S is placed at a distance L in front of the centre of plane mirror of width d which is hanging vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror, at a distance 2L as shown below. The distance over which the man can see the image of the light source in the mirror is nd then value of n is :
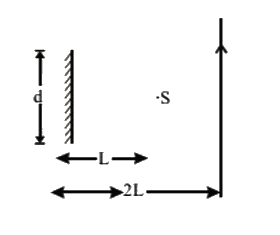View Solution