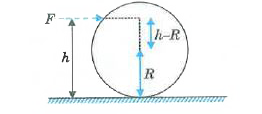
A uniform sphere of mass m and radius R is placed on a rough horizontal surface. The sphere is struck horizontally at a heighth from the floor. Match the following:

The sphere will roll without slipping if
ω=vR
Moment of inertia about diameter is
I=25MR2
Angular momentum of the sphere about C.M. is given by
Mv(h−R)=Iω
=25MR2⋅vR
or mv(h−R)=24MvR
or h=77R
So, if force is applied at h=75R sphere will roll without slipping
Torque due to sphere about CMτ=F(h−R). sphere will have only translational motion if t=0orh=R. Sphere will spin clockwise if torque is positive and will spin anticlockwise if torque is negative.
So (a)→(iii),(b)→(iv),(c)→(ii),(d)→(i).
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL QUESTIONS WITH ANSWERS
13 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - REVISION EXERCISES (Very Short Answer Questions Carrying 1 mark)
29 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS (OBJECTIVES QUESTIONS) (MULTIPLE CHOICE QUESTIONS (TYPE-I))
13 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A uniform sphere of mass m and radius R is placed on a rough horizontal surface [Fig.] The sphere is struck horizontally at a hight h from the floor. Match the following :
(a) h=R/2 (i) Sphere rolls without slipping with a constant velocity and no loss of energy.
(b) h=R (ii) Sphere spins clockwise, loses energy by friction.
(c ) h=3R/2 (iii) Sphere spins anti-clockwise, loses energy by friction.
(d) h=7R/5 (iv) Sphere has only a translational motion, looses energy by friction.

View SolutionA unifrom sphere of mass m and radius R is placed on a rough horizontal surface (figure) .the sphere is stuuck horizontally at a height h from the floor . Match the following

View Solution
Knowledge Check
A uniform sphere of mass m and radius R is placed on a rough horizontal surface [Fig.] The sphere is struck horizontally at a hight h from the floor. Match the following :
(a) h=R/2 (i) Sphere rolls without slipping with a constant velocity and no loss of energy.
(b) h=R (ii) Sphere spins clockwise, loses energy by friction.
(c ) h=3R/2 (iii) Sphere spins anti-clockwise, loses energy by friction.
(d) h=7R/5 (iv) Sphere has only a translational motion, looses energy by friction.
 AA -r, B - s, C - q, D - pBA - s, b - p, C - r, D - qCA - q, B - r, C - p, D - sDA - p, B - q, C - s, D - r
AA -r, B - s, C - q, D - pBA - s, b - p, C - r, D - qCA - q, B - r, C - p, D - sDA - p, B - q, C - s, D - rA solid sphere of mass M and radius R is placed on a rough horizontal surface. It is stuck by a horizontal cue stick at a height h above the surface. The value of h so that the sphere performs pure rolling motion immediately after it has been stuck is
 A2R5B5R2C7R5D9R5
A2R5B5R2C7R5D9R5A uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
A uniform sphere of mass m and radius R is placed on a rough horizontal surface. The spher is struck horizontally at a height h from the floor. Show that the sphere rolls without slipping with a constant velocity, when h=7R/5.
View SolutionA solid sphere of mass M and radius R is placed on a rough horizontal surface. It is stuck by a horizontal cue stick at a height h above the surface. The value of h so that the sphere performs pure rolling motion immediately after it has been stuck is

View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
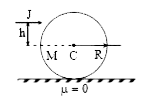
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View Solution
