Derive an expression for the moment of inertia of thin uniform rod about an axis passing through its one end. Also find the radius of gyration.
To derive the expression for the moment of inertia of a thin uniform rod about an axis passing through one of its ends, we will follow these steps:
Step 1: Define the system
Consider a thin uniform rod of length L and mass M. The linear mass density λ of the rod is given by:
λ=ML
This means that for every unit length of the rod, there is a mass of λ kg/m.
Step 2: Consider an elemental mass
Take a small elemental length dx at a distance x from the axis of rotation (which is at one end of the rod). The mass of this small element dm can be expressed as:
dm=λ⋅dx=ML⋅dx
Step 3: Calculate the moment of inertia of the elemental mass
The moment of inertia dI of the elemental mass dm about the axis is given by:
dI=dm⋅x2
Substituting for dm:
dI=(ML⋅dx)⋅x2=ML⋅x2⋅dx
Step 4: Integrate to find the total moment of inertia
To find the total moment of inertia I of the rod, integrate dI from x=0 to x=L:
I=∫L0dI=∫L0ML⋅x2⋅dx
This can be simplified as:
I=ML∫L0x2⋅dx
The integral ∫L0x2⋅dx can be calculated as:
∫L0x2⋅dx=(x33)L0=L33
Substituting this back into the equation for I:
I=ML⋅L33=ML23
Step 5: Find the radius of gyration
The radius of gyration K is defined by the relation:
I=MK2
Substituting our expression for I:
ML23=MK2
Dividing both sides by M (assuming M≠0):
K2=L23
Taking the square root gives:
K=L√3
Final Results
The moment of inertia of the thin uniform rod about an axis passing through one of its ends is:
I=ML23
And the radius of gyration is:
K=L√3
Consider a thin uniform rod of length L and mass M. The linear mass density λ of the rod is given by:
λ=ML
This means that for every unit length of the rod, there is a mass of λ kg/m.
Take a small elemental length dx at a distance x from the axis of rotation (which is at one end of the rod). The mass of this small element dm can be expressed as:
dm=λ⋅dx=ML⋅dx
The moment of inertia dI of the elemental mass dm about the axis is given by:
dI=dm⋅x2
Substituting for dm:
dI=(ML⋅dx)⋅x2=ML⋅x2⋅dx
To find the total moment of inertia I of the rod, integrate dI from x=0 to x=L:
I=∫L0dI=∫L0ML⋅x2⋅dx
This can be simplified as:
I=ML∫L0x2⋅dx
The integral ∫L0x2⋅dx can be calculated as:
∫L0x2⋅dx=(x33)L0=L33
Substituting this back into the equation for I:
I=ML⋅L33=ML23
The radius of gyration K is defined by the relation:
I=MK2
Substituting our expression for I:
ML23=MK2
Dividing both sides by M (assuming M≠0):
K2=L23
Taking the square root gives:
K=L√3
The moment of inertia of the thin uniform rod about an axis passing through one of its ends is:
I=ML23
And the radius of gyration is:
K=L√3
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - REVISION EXERCISES (Numerical Problems)
20 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
67 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - REVISION EXERCISES (Short Answer Questions Carrying 2 or 3 marks)
22 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Derive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionState an expression for the moment of inertia of a solid uniform disc rotating about an axis passing through its centre, perpendicular to its plane. Hence derive an expression for the moment of inertia and radius of gyration.
(i) about a tangent in the plane of the disc, and
(ii) about a tangent perpendicular to the plane of the disc. In a set, 21 tuning forks are arranged in a series of decresing frequencies. Each tuning fork produces 4 beats per second with the preceding fork. If the first fork is an octave of the last fork , find the frequencies of the first and tenth forks.
View Solution
Knowledge Check
Figure shows the variation of the moment of inertia of a uniform rod, about an axis passing through itss centre and inclined at an angle θ to the length. The moment of inertia of the rod about an axis passing through one of its ends and making an angle θ=π3 will be
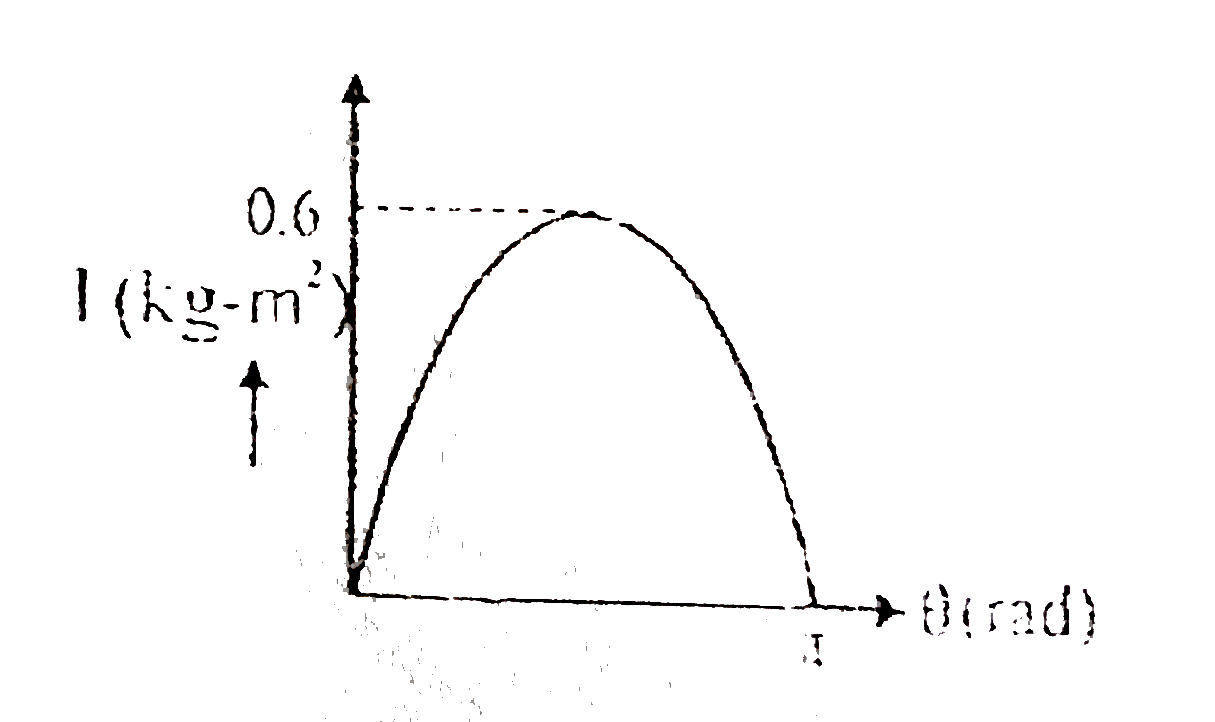 A0.45kg−m2B1.8kg−m2C2.4kg−m2D1.5kg−m2
A0.45kg−m2B1.8kg−m2C2.4kg−m2D1.5kg−m2A thin rod of mass M and length L is bent into a circular ring. The expression for moment of inertia of ring about an axis passing through its diameter is
AML22π2BML24π2CML28π2DML2π2The radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
AL√12BL2√12CL√3DL√2
The moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionState the expression for the moment of inertia of a thin uniform disc about an axis perpendicular to its plane and through its centre. Hence deduce the expression for its moment of inertia about a tangential axis perpendicular to its plane.
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionThree identical thin rods, each of mass m and length l, are joined to form an equilateral triangular frame. Find the moment of inertia of the frame about an axis parallel to tis one side and passing through the opposite vertex. Also find its radius of gyration about the given axis.
View SolutionA uniform rod of length 1 metre has a mass of 500gram. What is moment of inertia of the rod about an axis passing through the centre of the rod perpendicular to its length. How is moment of inertia changed when the same axis passes through one end of the rod ?
View Solution
