A sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
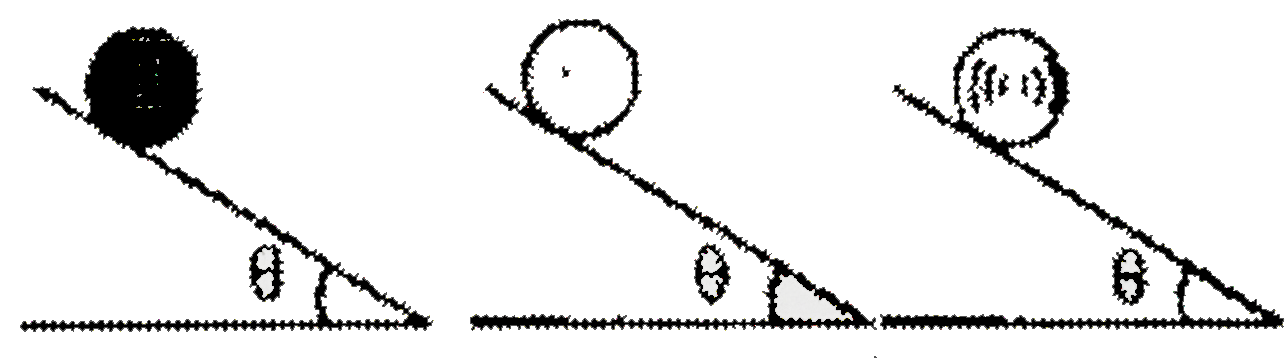
Which of the follwing order is true for final KE of the bodies?
Solid sphere reaches the bottom with minimum K.E.
Disc reaches the bottom with minimum K.E.
Hollow sphere reaches the bottom with minimum K.E.
All three objects reach the bottom with same K.E.
Since it is a case of pure rolling hence total mechanical energy remains constant. All the objects are released from the same height h (say), then all will reach the bottom with kinetic energy mgh. Hence option (d) is correct.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )48videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )35videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - REVISION EXERCISES (Numerical Problems)20videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A solid sphere, a hollow sphere, a solid disc and a hollow cylinder are allowed to roll down a sufficiently rough inclined plane starting from rest. All have same mass and radius.
 View Solution
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be :-
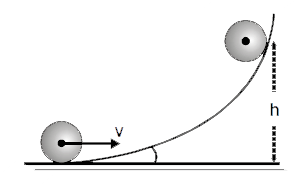 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.

Which of the following order is' true for tiine taken by the bodies to reach the bottom of incline?Asphere > disc > ringBring > disc > sphereCdisc > ring > sphereDdisc = ring = sphere - Question 2 - Select One
A sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
Which of the following order is true for final linear velocity of the bodies?Asphere > disc > ringBring > disc > sphereCdisc > ring > sphereDdisc = ring = sphere - Question 3 - Select One
A sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
Which of the following order is true for frjctional force acting on the bodies during their rolling?Asphere > disc > ringBring > disc > sphereCdisc > ring > sphereDdisc = ring = sphere
A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 View Solution
View SolutionA solid sphere, disc and solid cylinder, all of the same mass, are allowed to roll down (from rest) on inclined plane, them
View SolutionA sphere and circular disc of same mass and radius are allowed to roll down an inclined plane from the same height without slipping. Find the ratio of times taken by these two to come to the bottom of incline :
View SolutionAsphere, a disc and a ring of the same mass but of different density and radii are allowed to roll down on an inclined plane without slipping simultaneously, through the same height, then:
View SolutionA sphere and circular disc of same mass and radius are allowed to roll down an inclined plane from the same height without slipping. Find the ratio of times taken by these two to come to the bottom of incline :
View Solution

