A solid cylinder of mass 2 kg and radius 50 cm rolls up an inclined plane of angle of inclination 30∘. The centre of mass of the cylinder has speed of 4 m/s. The distance travelled by the cylinder on the inclined surface will be, [ take g=10m/s2]
2.4m
2.2m
1.6m
1.2m
The correct Answer is:A
Using energy conservation we can write the following:
34mv2=mgh⇒h=3v24g=3×(4)24×10=1.2m
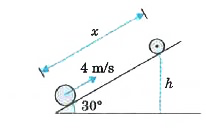
Now, 34mv2=mgh⇒h=3v24g=3×(4)24×10=1.2m
x=2.4 m
Hence option (a) is correct.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
48 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
35 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - REVISION EXERCISES (Numerical Problems)
20 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. force of friction on the cylinder is?
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution
Knowledge Check
A solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.A solid cylinder rolls up an inclined plane of angle of inclination 30∘ . At the bottom of the inclined plane the centre of mass of the cylinder has a speed of 5ms−1 . How far will cylinder go up the plane ?
(Take g = 10ms−2)A154mB415 mC103 mD310 mA solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
A√(2gh)B√4/3.ghC√3/4.ghD√(4g/h)
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA solid cylinder of mass 500 g and radius 10 cm rolls down an inclined plane of inclination 1 in 10. Calculate its acceleration and total energy after 6 s.
View SolutionA solid cylinder rolls up an inclined plane of angle of inclination 30∘. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5m/s.
(a) How far will the cylinder go up the plane ? (B) How long will it take to return to the bottom ?
View SolutionA sphere rolls up an inclined plane whose inclination is 30∘. At the bottom of the inclined plane, the center of mass of the sphere has a translational speed of 5ms−1 (a) How far does the sphere travel up the plane? (b) How long does it take to return to the bottom?
View SolutionA solid cylinder rolls up an inclined plane of angle of inclinátion 30∘. At the bottom of the inclined plane the centre of mass of the cylinder has a speed of 5 m / s. How long (in seconds) will it take to return to the bottom? [Take g=10 m / (s)2],
View Solution
