The moment of inertia of a uniform cylinder of length $l and r a d i u s R$ about its perpendicular bisector is $I$ . What is the ratio $l / R$ such that the moment of inertia is minimum ?

A

$\sqrt{\frac{3}{4}}$

B

$\frac{s q r (3)}{2}$

C

1

D

$\frac{3}{s \sqrt{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

We need to calculate the moment of inertia of the cylinder about its perpendicular bisector.
Consider the following figure:
Let the mass of the cylinder be M.

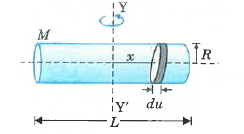
Let us take a segment of the cylinder of thickness dx at a distance x from the axis of rotation YY.
The segment chosen here is like a disc of radius R. As it is given that there is uniform mass distribution, hence the mass of the disc can be written as:
$d M = (\frac{M}{π R^{2} l}) (π R^{2} d x) = (\frac{M}{l}) d x$
We know that the moment of inertia of a disc of mass m and radius r about its diameter is given by
$I = \frac{m r^{2}}{4}$
The moment of inertia of the segment disc about its diameter is $d I_{1} = \frac{d M R^{2}}{4}$
Applying parallel axis theorem, the moment of inertia of the segment disc about the axis YY. can be calculated as:
$d I = \frac{d M R^{2}}{4} + d M x^{2} = \frac{M R^{2}}{4 l} d x + \frac{M}{l} x^{2} d x$
We can calculate the moment of inertia of the cylinder by integration as follows:
$I = \int d I = \int_{- l / 2}^{+ l / 2} \frac{M R^{2}}{4 l} d x + \int_{- l / 2}^{+ l / 2} \frac{M}{l} x^{2} d x$
$I = \frac{M R^{2}}{4 l} [\frac{l}{2} - (- \frac{l}{2})] + \frac{M}{3 l} [{(\frac{1}{2})}^{3} - {(- \frac{l}{2})}^{3}]$
$I = \frac{M R^{2}}{4} + \frac{M l^{2}}{12} ... ... (i)$
For the moment of inertia to be minimum, $\frac{d I}{d l} = 0$
In the equation (i) we shall express the radius R of the cylinder in terms of its length l.
Let the mass density of the cylinder be $ρ$ .
That means:
$ρ = \frac{M}{π R^{2} l}$
$\Rightarrow R^{2} = \frac{M}{π l ρ}$
Substituting $R^{2}$ in equation (i)
$I = \frac{M}{4} = (\frac{M}{π l ρ}) + \frac{M l^{2}}{12} = \frac{M^{2}}{4 π l ρ} + \frac{M l^{2}}{12}$
Differentiating both sides:
$\frac{d I}{d l} = \frac{d}{d l} (\frac{M^{2}}{4 π l ρ}) + \frac{d}{d l} (\frac{M l^{2}}{12})$
$= (\frac{M^{2}}{4 π ρ}) (- 1) l^{- 2} + \frac{M l}{6}$
$= \frac{M l}{6} - (\frac{M^{2}}{4 π ρ l^{2}})$
For maxima or minima,
$\frac{d I}{d l} = 0$
$\frac{M l}{6} - (\frac{M^{2}}{4 π ρ l^{2}}) = 0$
$\frac{l^{3}}{3} = (\frac{M}{2 π ρ})$
Substituting
$ρ = \frac{M}{π R^{2} l}$
$\frac{l^{3}}{3} = ⎛ ⎜ ⎜ ⎝ \frac{M}{2 π (\frac{M}{π R^{2} l})} ⎞ ⎟ ⎟ ⎠$
$\frac{l^{3}}{3} = ⎛ ⎜ ⎜ ⎝ \frac{1}{2 (\frac{1}{R^{2} l})} ⎞ ⎟ ⎟ ⎠$
$\frac{l^{3}}{3} = (\frac{R^{2} l}{2})$
$\frac{l^{2}}{R^{2}} = \frac{3}{2}$
$\Rightarrow \frac{l}{R} = \sqrt{\frac{3}{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Moment of inertia of a hollow cylinder of mass M and radius r about its own axis is
A $\frac{2}{3} M r^{2}$
B $M r^{2}$
C $\frac{1}{3} M r^{2}$
D $\frac{1}{2} M r^{2}$
Question 2 - Select One
The moment of inertia of a uniform circular disc of mass M and of radius R about one of its diameter is
A $\frac{1}{4} M R^{2}$
B $\frac{1}{2} M R^{2}$
C $\frac{2}{3} M R^{2}$
D $\frac{2}{5} M R^{2}$
Question 3 - Select One
Moment of inertia of a hollow cylinder of mass $M$ and radius $R$ , about the axis of cylinder is
A $\frac{1}{2} M R^{2}$
B $M R^{2}$
C $\frac{2}{3} M R^{2}$
D $\frac{2}{5} M R^{2}$

MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )

Home
Ask Doubt
Profile