State and explain Torricelli's theorem.
Step-by-Step Solution:
1. Understanding the Concept: Torricelli's theorem, also known as Torricelli's law, relates to fluid dynamics and describes the speed of fluid flowing out of an opening under the influence of gravity.
2. State the Theorem: Torricelli's theorem states that the speed (v) of a fluid flowing out of a hole at a depth (h) from the surface of the fluid is given by the equation:
v=√2gh
where:
- v = speed of the fluid exiting the hole,
- g = acceleration due to gravity (approximately 9.81m/s2),
- h = height of the fluid column above the hole.
3. Explanation of the Theorem: The theorem can be understood by considering that the fluid at a height h possesses potential energy due to its elevation. When the fluid exits through the hole, this potential energy is converted into kinetic energy. The speed of the fluid as it exits is equivalent to the speed that an object would attain if it were to fall freely from the same height h.
4. Derivation of the Equation: To derive the equation, we can use the principle of conservation of energy:
- The potential energy (PE) at height h is given by:
PE=mgh
- The kinetic energy (KE) of the fluid as it exits is given by:
KE=12mv2
- Setting the potential energy equal to the kinetic energy gives:
mgh=12mv2
- Simplifying this equation (and canceling m from both sides) leads to:
gh=12v2
- Rearranging gives:
v2=2gh
- Taking the square root results in:
v=√2gh
5. Conclusion: Torricelli's theorem provides a fundamental understanding of how fluids behave when exiting a container. It highlights the relationship between gravitational potential energy and kinetic energy in fluid dynamics.
---
v=√2gh
where:
- v = speed of the fluid exiting the hole,
- g = acceleration due to gravity (approximately 9.81m/s2),
- h = height of the fluid column above the hole.
- The potential energy (PE) at height h is given by:
PE=mgh
- The kinetic energy (KE) of the fluid as it exits is given by:
KE=12mv2
- Setting the potential energy equal to the kinetic energy gives:
mgh=12mv2
- Simplifying this equation (and canceling m from both sides) leads to:
gh=12v2
- Rearranging gives:
v2=2gh
- Taking the square root results in:
v=√2gh
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Long Answer Questions)
7 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Numerical Problems)
28 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Fill in the Blanks)
10 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
Knowledge Check
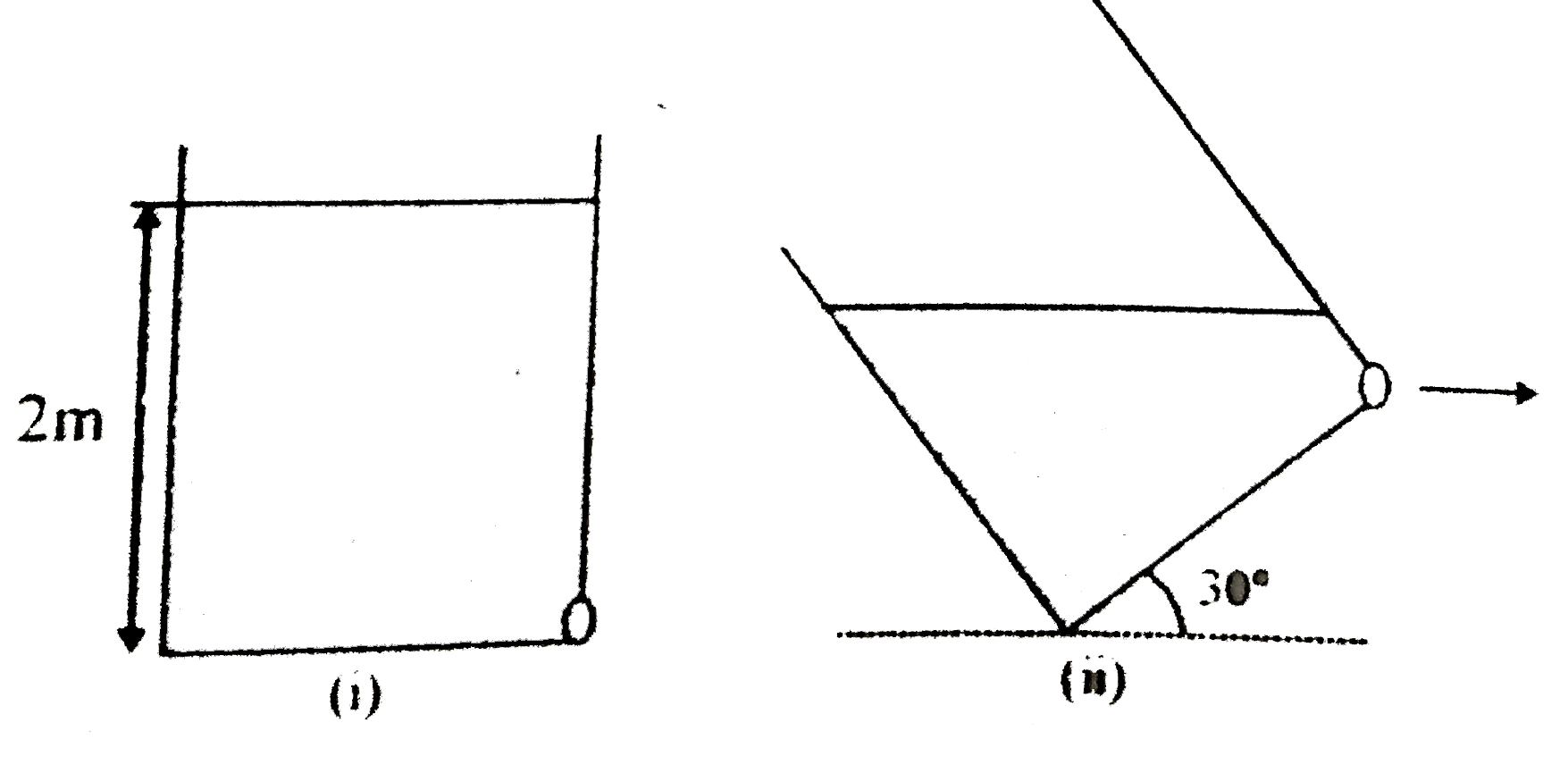
Velocity of efflux in torricelli's theorem is given by v=√2gh, here h is the height of hole from the top surface, after that, motion of liquid can be treated as projectile motion. Liquid is filled in a vessel of square base (2m×2m) upto a height of 2m as shown in figure (i). in figure (ii) the vessel is tilted from horizontal at 30∘ what is the velocity of efflux in this case ? Liquid does not spills out?A3.29m/sB4.96m/sC5.67m/sD2.68m/s
State and explain Stefan's law.
View SolutionState and explain Charles'law.
View Solution_S01_073_Q01.png)
Velocity of efflux in torricelli's theorem is given by v=√2gh here h is the height of hole from the top surface, after that motion of liquid can be treated as projectile motion.
Q. What is its time of fall of liquid on the ground?
(a). 1√2s
(b). 1√3s
(c). 1√5s
(d). √2s
View Solution_S01_074_Q01.png)
Velocity of efflux in torricelli's theorem is given by v=√2gh here h is the height of hole from the top surface, after that motion of liquid can be treated as projectile motion.
Q. At what distance from point O, will be strike on the ground?
(a). 5.24 m
(b). 6.27 m
4.93 m
(d). 3.95 m
View SolutionState and explain law of Malus.
View SolutionState and prove Bernoulli's theorem.
View SolutionState and explain principle of heat exchange.
View Solution
