Three rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
35∘C
47∘C
51∘C
57∘C
The correct Answer is:B
To find the temperature at the junction of the three rods, we can follow these steps:
Step 1: Understand the setup
We have three rods made of the same material, with equal cross-sectional areas and lengths. The rods are connected in such a way that they form a junction. The temperatures at the ends of the rods are given as T1=70∘C and T2=0∘C.
Step 2: Identify thermal resistance
The thermal resistance R for each rod can be expressed as:
R=LkA
where L is the length of the rod, k is the thermal conductivity of the material, and A is the cross-sectional area. Since all rods have the same length, area, and material, the thermal resistance for each rod is the same, denoted as R.
Step 3: Apply the junction law
According to the junction law, the heat flow through each rod must be equal at the junction. We can express this as:
T−T1R+T−T2R+T−T3R=0
where T is the temperature at the junction, T1 is the temperature of the first rod, T2 is the temperature of the second rod, and T3 is the temperature of the third rod.
Step 4: Substitute known values
Assuming the third rod is at T3=0∘C (as per the problem statement), we can substitute the values:
T−70R+T−0R+T−0R=0
Step 5: Simplify the equation
This simplifies to:
T−70R+TR+TR=0
Multiplying through by R (since R≠0):
T−70+T+T=0
This leads to:
3T−70=0
Step 6: Solve for T
Rearranging gives:
3T=70
T=703≈23.33∘C
Step 7: Conclusion
Thus, the temperature at the junction of the rods is approximately:
T≈23.33∘C
We have three rods made of the same material, with equal cross-sectional areas and lengths. The rods are connected in such a way that they form a junction. The temperatures at the ends of the rods are given as T1=70∘C and T2=0∘C.
The thermal resistance R for each rod can be expressed as:
R=LkA
where L is the length of the rod, k is the thermal conductivity of the material, and A is the cross-sectional area. Since all rods have the same length, area, and material, the thermal resistance for each rod is the same, denoted as R.
According to the junction law, the heat flow through each rod must be equal at the junction. We can express this as:
T−T1R+T−T2R+T−T3R=0
where T is the temperature at the junction, T1 is the temperature of the first rod, T2 is the temperature of the second rod, and T3 is the temperature of the third rod.
Assuming the third rod is at T3=0∘C (as per the problem statement), we can substitute the values:
T−70R+T−0R+T−0R=0
This simplifies to:
T−70R+TR+TR=0
Multiplying through by R (since R≠0):
T−70+T+T=0
This leads to:
3T−70=0
Rearranging gives:
3T=70
T=703≈23.33∘C
Thus, the temperature at the junction of the rods is approximately:
T≈23.33∘C
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) AIMPMT/NEET AND OTHER STATE BOARDS FOR MEDICAL ENTRANCE)
18 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) JEE MAIN AND OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
19 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - REVISION EXERCISE (NUMERICAL PROBLEM)
19 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)
16 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Three rods of same material, same area of cross section but different lengths 10 cm, 20 cm and 30 cm are connected at a point as shown. What is temperature of junction O?
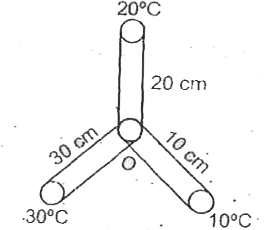
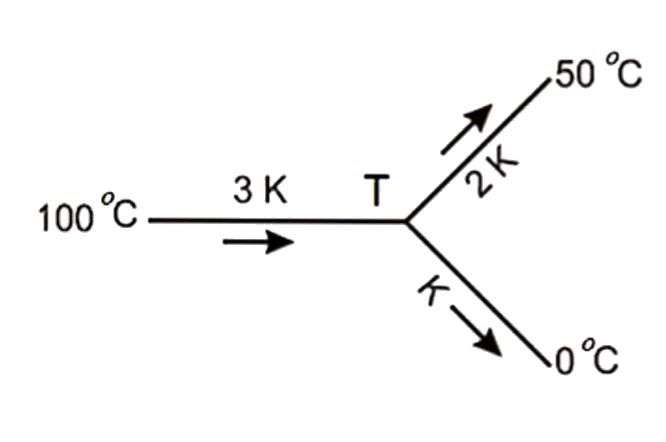
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
View Solution
Knowledge Check
Four identical heat conductors are connected as shown in the figure. The temperature θ of the junction is [rods are insulated from the sides ]
 A30∘CB15∘CC60∘CD70∘C
A30∘CB15∘CC60∘CD70∘CThree rods made of the same material and having same cross-section area but different length 10 cm, 20 cm and 30 cm are joined as shown. The temperature of the junction is
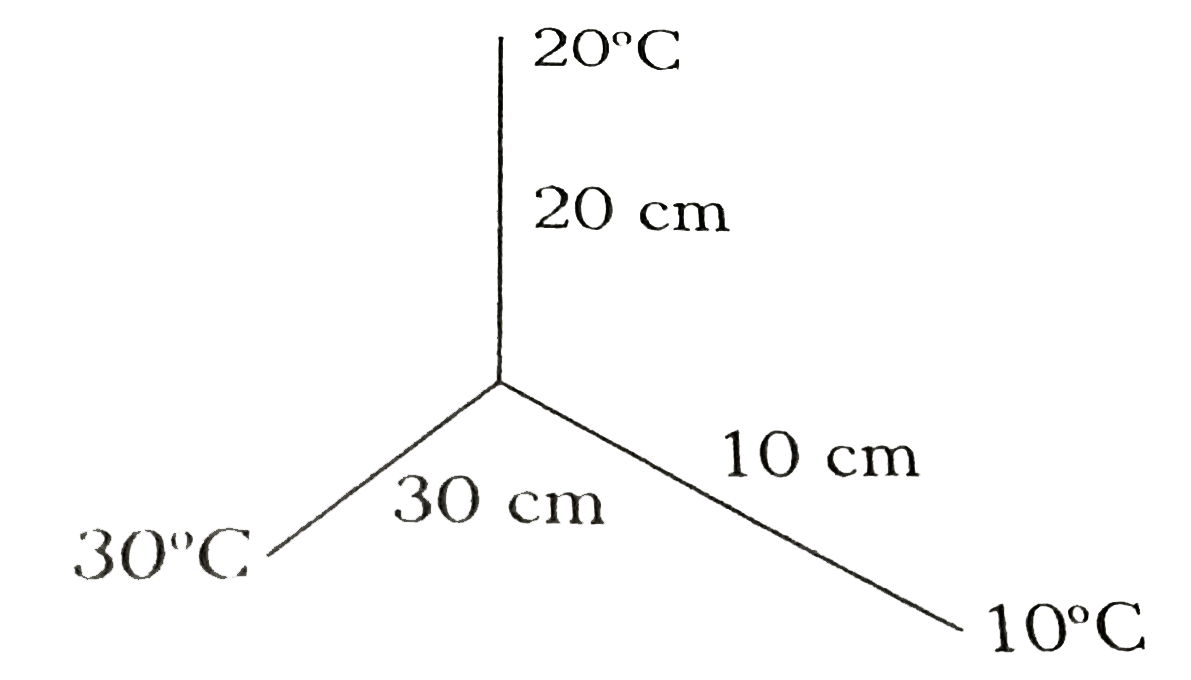 A10.8∘CB14.6∘CC16.4∘CD18.2∘C
A10.8∘CB14.6∘CC16.4∘CD18.2∘CThree rods are made from the same material and having the same cross-sectional area and length have been joined as shown in the figure.
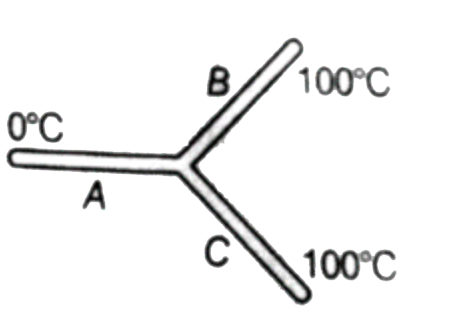
The left end and right end are kept 0∘Cand100∘C , respectively . The temperature of the junction of three rods will beA50∘CB60∘CC80∘CD66.66∘C
Three rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.

There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View SolutionThree rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below

Then , the temperature of the junction in steady - state is
View SolutionTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.

View SolutionThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
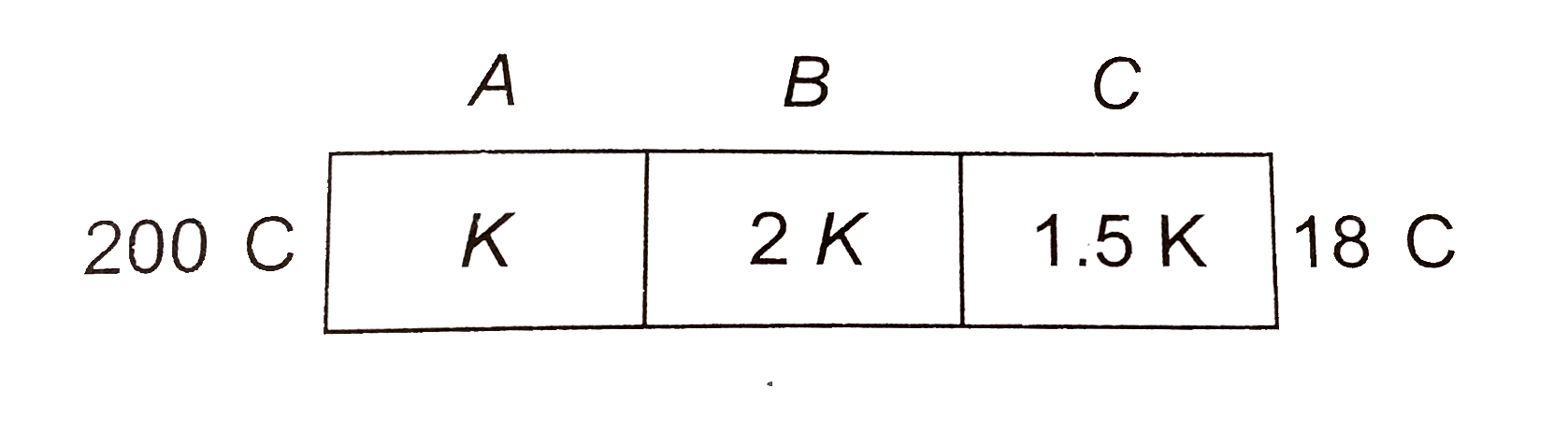
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is

View Solution
