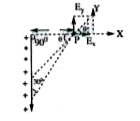
Calculate electric field intensity at point P due to a thin positive uniformly charged rod . Point P is at perpendicular distance d from the rod . The lower and upper ends of the rod make the angles $α$ and $β$ as shown below .

Text Solution

Verified by Experts

Refer the given figure . Let us select one segment of length dy at a distance y from O. Electric field due to this segment is $d \to E$ as shown. We have $λ$ as linear charge density .So the charge on segment is $λ d y$ .
$d E = \frac{1}{4 π ε_{0}} \frac{λ d y}{d^{2} + y^{2}}$
The direction of $d \to E$ is dissimilar for different locations of the segment . Hence $d \to E$ cannot be integrated directly. So, we shall integrate components perpendicular and parallel to rod separately .
$E_{x} = \int d E cos θ = \frac{λ}{4 π ε_{0}} \int \frac{d y}{d^{2} + y^{2}} cos θ$
$E_{y} = \int d E sin θ = \frac{λ}{4 π ε_{0}} \int \frac{d y}{d^{2} + y^{2}} sin θ$
To solve above integrations, let us assume :
$y = d tan θ$
$d y = d {sec}^{2} θ d θ$
$d^{2} + y^{2} = d^{2} {sec}^{2} θ$
$\frac{d y}{d^{2} + y^{2}} = \frac{d θ}{d}$
On substituting ,
$E_{x} = \int d E cos θ - \frac{λ}{4 π ε_{0} d} \int_{- α}^{β} cos θ d 0$
$E_{y} = \int d E sin θ = \frac{λ}{4 π ε_{0} d} \int_{- α}^{β} sin θ d θ$
In the above integration , the limits are taken from $θ = - α$ corresponding to lower end of rod . And $θ = β$ for the upper end of the rod .
On solving both, we get the following :
$E_{x} = \int d E cos θ = \frac{λ}{4 π ε_{0} d} \int_{- α}^{β} cos θ d θ = \frac{λ}{4 π ε_{0} d} {[sin θ]}_{- α}^{β}$
$= \frac{λ}{4 π ε_{0} d} [sin β - sin (- α)]$
$E_{y} = \int d E sin θ = \frac{λ}{4 π ε_{0} d} \int_{- α}^{β} sin θ d θ = \frac{λ}{4 π ε_{0} d} {[- cos θ]}_{- α}^{β}$
$= \frac{λ}{4 π ε_{0} d} [(- cos β) - (- cos (- α))]$
$E_{x} = \frac{λ}{4 π ε_{0} d} (sin α + sin β) E_{x}$ represents the component, perpendicular to rod in the direction away from the rod for $λ > 0 . E_{y} = \frac{λ}{4 π ε_{0} d} (cos α - cos β)$
$E_{y}$ represents component that is parallel to the rod . The direction of $E_{y}$ can be upwards or downwards depending on the values of $α$ and $β$ .

Updated on:21/07/2023

The expression for electric field intensity at a points outside uniformly charged thin plane sheet is (where, d is the distance of point from plane sheet)
Aindependent of d
Bdirectly proportional to $\sqrt{d}$
Cdirectly proportional to d
Ddirectly proportional to $\frac{1}{\sqrt{d}}$
The direction $(θ)$ of $\to E$ at point P due to uniformly charged finite rod will be

AAt an angle $30^{\circ}$ from the x-axis
B $45^{\circ}$ from the x-axis
C $60^{\circ}$ from the x-axis
Dnone of these