Two identical charge of magnitude +2 μCare kept on two diagonally opposite vertices of a square of side a. Both the charges are joined using an insulated massless chord. What will be the tension in the chord? Neglect the gravitational forces involved.
To find the tension in the chord connecting two identical charges of magnitude +2 µC placed at diagonally opposite vertices of a square of side 'a', we can follow these steps:
1. Identify the Charges and Their Positions:
- Let the two charges be q1=q2=+2μC=2×10−6C.
- Place the charges at diagonally opposite corners of a square with side length a.
2. Calculate the Distance Between the Charges:
- The distance r between the two charges (diagonal of the square) can be calculated using the Pythagorean theorem:
r=a√2
3. Apply Coulomb's Law:
- According to Coulomb's law, the force F between two point charges is given by:
F=kq1q2r2
- Here, k (Coulomb's constant) is 14πϵ0, where ϵ0 is the permittivity of free space.
4. Substituting the Values:
- Substitute q1 and q2 into the formula:
F=k(2×10−6)2(a√2)2
- Simplifying the denominator:
(a√2)2=2a2
- Therefore, the force becomes:
F=k(2×10−6)22a2
5. Calculate the Force:
- Plugging in the value of k:
F=14πϵ0(2×10−6)22a2
- This simplifies to:
F=(2×10−6)28πϵ0a2
6. Determine the Tension in the Chord:
- Since the charges are in equilibrium and not moving, the tension T in the chord must equal the force F exerted by the charges on each other:
T=F
- Therefore, the tension in the chord is:
T=(2×10−6)28πϵ0a2
7. Final Expression:
- Substituting ϵ0≈8.85×10−12C2/N m2:
T=(4×10−12)8π(8.85×10−12)a2
- This can be simplified further if necessary, but the expression gives the tension in terms of a.
- Let the two charges be q1=q2=+2μC=2×10−6C.
- Place the charges at diagonally opposite corners of a square with side length a.
- The distance r between the two charges (diagonal of the square) can be calculated using the Pythagorean theorem:
r=a√2
- According to Coulomb's law, the force F between two point charges is given by:
F=kq1q2r2
- Here, k (Coulomb's constant) is 14πϵ0, where ϵ0 is the permittivity of free space.
- Substitute q1 and q2 into the formula:
F=k(2×10−6)2(a√2)2
- Simplifying the denominator:
(a√2)2=2a2
- Therefore, the force becomes:
F=k(2×10−6)22a2
- Plugging in the value of k:
F=14πϵ0(2×10−6)22a2
- This simplifies to:
F=(2×10−6)28πϵ0a2
- Since the charges are in equilibrium and not moving, the tension T in the chord must equal the force F exerted by the charges on each other:
T=F
- Therefore, the tension in the chord is:
T=(2×10−6)28πϵ0a2
- Substituting ϵ0≈8.85×10−12C2/N m2:
T=(4×10−12)8π(8.85×10−12)a2
- This can be simplified further if necessary, but the expression gives the tension in terms of a.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions51videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Tough & Tricky Problems20videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test15videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST15videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION14videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Two identical charges of magnitude 0.4 mC are placed on diagonally opposite vertices of a square of side 10 cm. Calculate the amount of work done in slowly moving one of the charges from diagonally opposite vertex to adjacent vertex.
View SolutionTwo point charges −0.1μCand0.2μC are placed on diagonally opposite vertices of a square of side 15 cm. Locate a point P on the diagonal, where electric potential is zero. Consider the potential infinity to be zero.
View Solution
Knowledge Check
- Question 1 - Select One
Three point charges each of value +q are placed on three vertices of a square of side a metre. What is the magnitude of the force on a point charge of value −q coulomb placed at the centre of the square?
A(14πε0)(qa)2B(12πε0)(2qa)2C(12πε0)(qa)2D(14πε0)(2qa)2 - Question 2 - Select One
Four charges q1=1μC,q2=2μC,q3=−3μC and q4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
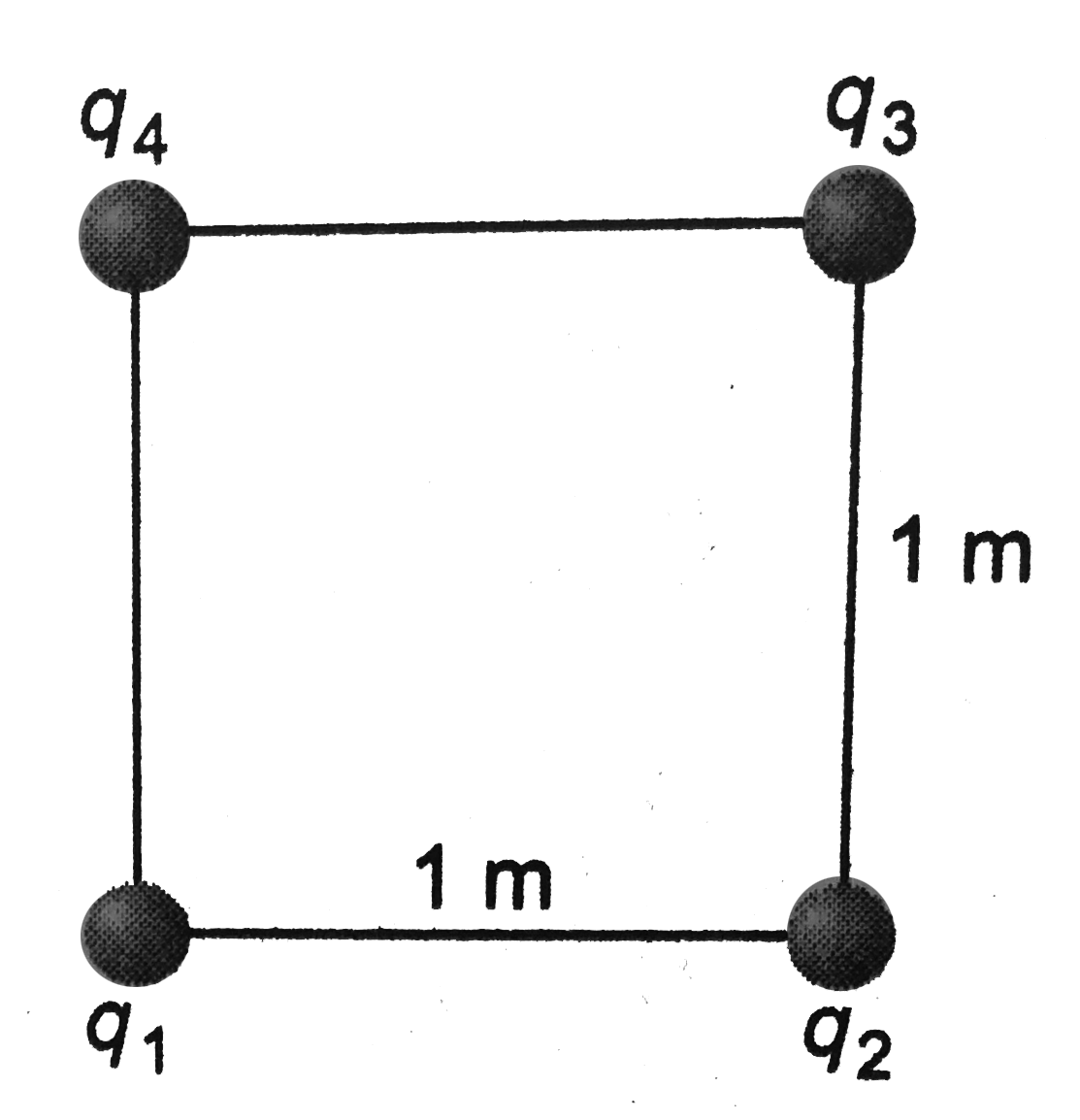 A−5.28×10−2JB−7.62×10−2JC−8.91×10−2JD−4.33×10−2J
A−5.28×10−2JB−7.62×10−2JC−8.91×10−2JD−4.33×10−2J - Question 3 - Select One
Two positive charges of magnitude q are placed at the ends of a side ( side 1) of a square of side 2a . Two negative charges of the same magnitude are kept at the other corners . Staring from rest , n a charge Q moves from the middle of side 1 to the centre of square , its kinetic energy at the centre of square is -.
A14π∈02qQa(1+1√5)B14π∈02qQa(1+1√5)C14π∈02qQa(1+1√5)D14π∈02qQa(1+1√5)
Two charges +0.4μC and−0.2μC are placed on adjacent vertices of a square of side 10 cm. Another charge of 1.2μC is placed at the centre af the square Calculate the force and its direction in the charge kept in the centre .
View SolutionTwo identical positive charges are placed at the diagonally opposite corners of a square and two more identical but negative charges are placed at the remaining two corners. What is the work done in putting all charges together at the centre if q is the magnitude of each charge and 2a is the length of each side of the square?
View SolutionThree identical charges of 2mC are kept on the vertices of an equilateral triangle of side 10 cm. A third charge of 1 mC is kept on the centroid of the triangle Calculate the force acting on the charge 1mC.
View SolutionTwo point charges of +q each are placed at two diagonally opposite corners of a square. Another two point charges of -q charge each are placed at the two remaining corners. Take the edge length of square equal to l. Calculate (i) work needed to move these charges slowly from an infinite separation to this given configuration. (ii) Assume that four charges at corners of the square are held fixed. Another charge Q is to be moved from infinity to the centre of this square slowly. What additional work is required to do so?
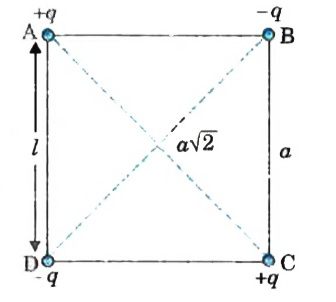 View Solution
View SolutionTwo positive charges of magnitude q are placed at the ends of a side (side 1 ) of square of side 2a. Two negative cahrges of the same magnitude ar kept at the other comers. Starting from rest, if the charge Q moves from the middle of side (1) to the centre of square , its kinetc energy at the centre of square is
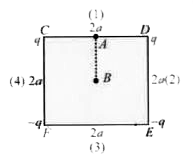 View Solution
View Solution

