A particle of mass 1 mg loses 108 electrons and then stays in equilibrium against gravity inside electric field. What should be the magnitude and direction of the electric field intensity?
To solve the problem, we need to find the magnitude and direction of the electric field intensity that allows a particle of mass 1 mg to remain in equilibrium against gravity after losing 10^8 electrons.
1. Identify the mass of the particle:
The mass of the particle is given as 1 mg. We convert this to kilograms:
m=1 mg=1×10−3 g=1×10−6 kg
2. Calculate the charge of the particle:
The particle loses 10^8 electrons. The charge of one electron is approximately e=1.6×10−19 coulombs. Therefore, the total charge lost is:
Q=n×e=108×1.6×10−19 C=1.6×10−11 C
Since the particle loses electrons, it becomes positively charged:
Q=+1.6×10−11 C
3. Calculate the gravitational force acting on the particle:
The gravitational force Fg acting on the particle can be calculated using the formula:
Fg=m×g
where g is the acceleration due to gravity, approximately 9.81 m/s2:
Fg=(1×10−6 kg)×(9.81 m/s2)=9.81×10−6 N
4. Set up the equilibrium condition:
For the particle to be in equilibrium, the upward electric force Fe must equal the downward gravitational force Fg:
Fe=Fg
The electric force can be expressed as:
Fe=Q×E
where E is the electric field intensity. Therefore, we have:
Q×E=m×g
5. Solve for the electric field intensity E:
Rearranging the equation gives:
E=FgQ=9.81×10−6 N1.6×10−11 C
Calculating this gives:
E=6.13125×105 N/C≈6.13×105 N/C
6. Determine the direction of the electric field:
Since the particle is positively charged and needs to move upward against gravity, the electric field must also be directed upwards.
Final Answer:
The magnitude of the electric field intensity required is approximately 6.13×105 N/C and its direction should be upwards.
The mass of the particle is given as 1 mg. We convert this to kilograms:
m=1 mg=1×10−3 g=1×10−6 kg
The particle loses 10^8 electrons. The charge of one electron is approximately e=1.6×10−19 coulombs. Therefore, the total charge lost is:
Q=n×e=108×1.6×10−19 C=1.6×10−11 C
Since the particle loses electrons, it becomes positively charged:
Q=+1.6×10−11 C
The gravitational force Fg acting on the particle can be calculated using the formula:
Fg=m×g
where g is the acceleration due to gravity, approximately 9.81 m/s2:
Fg=(1×10−6 kg)×(9.81 m/s2)=9.81×10−6 N
For the particle to be in equilibrium, the upward electric force Fe must equal the downward gravitational force Fg:
Fe=Fg
The electric force can be expressed as:
Fe=Q×E
where E is the electric field intensity. Therefore, we have:
Q×E=m×g
Rearranging the equation gives:
E=FgQ=9.81×10−6 N1.6×10−11 C
Calculating this gives:
E=6.13125×105 N/C≈6.13×105 N/C
Since the particle is positively charged and needs to move upward against gravity, the electric field must also be directed upwards.
The magnitude of the electric field intensity required is approximately 6.13×105 N/C and its direction should be upwards.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Tough & Tricky Problems
20 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Knowledge Check
Some equipotential surfaces are shown in figure . The magnitude and direction of electric field is
 A2V/cm at angle 120∘ with +ve x-axis in anticlockwise directionB2V/cm at angle 120∘ with +ve x-axis in clockwise directionC1V/cm at angle 150∘ with +ve x-axis in anticlockwise directionD1V/cm at an angle 120∘ with +ve x-axis in clockwise direction
A2V/cm at angle 120∘ with +ve x-axis in anticlockwise directionB2V/cm at angle 120∘ with +ve x-axis in clockwise directionC1V/cm at angle 150∘ with +ve x-axis in anticlockwise directionD1V/cm at an angle 120∘ with +ve x-axis in clockwise direction
Some equipotential surfaces are shown in figure. What can you say about the magnitude and the direction of the electric field ?
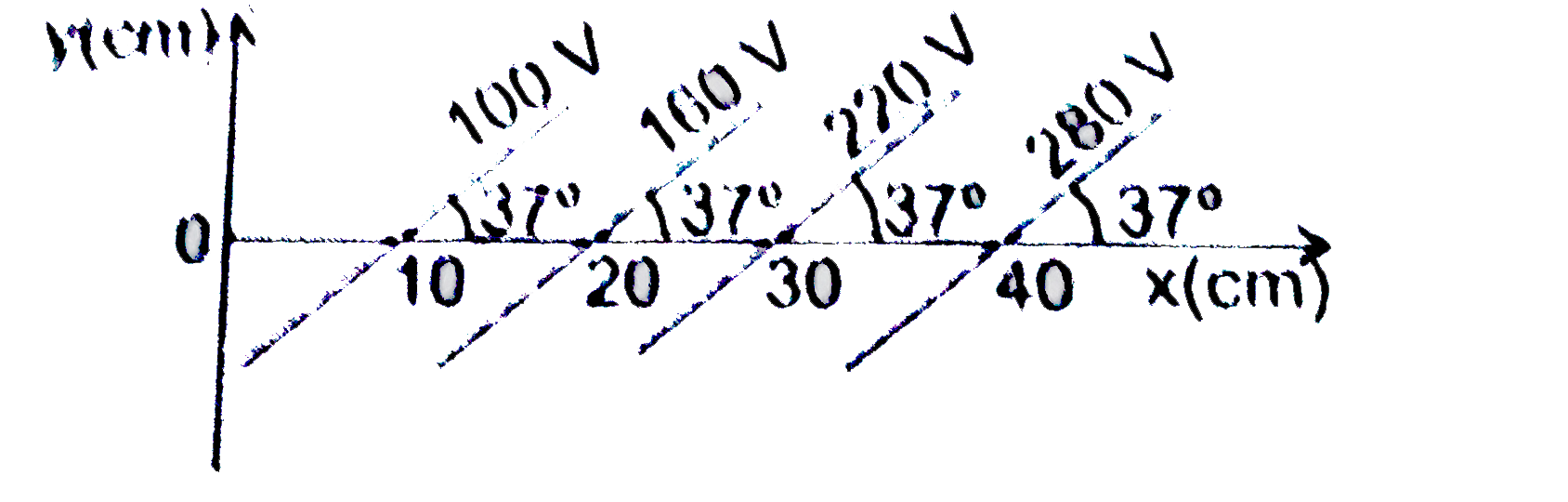
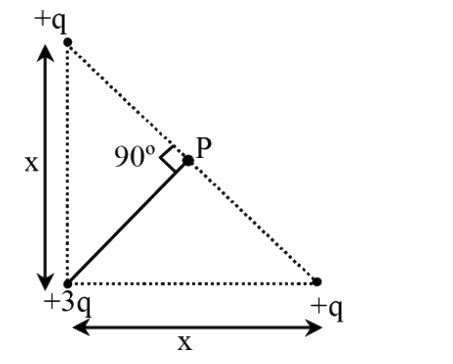
View SolutionThe magnitude and direction of the electric field at point P can be best represented by
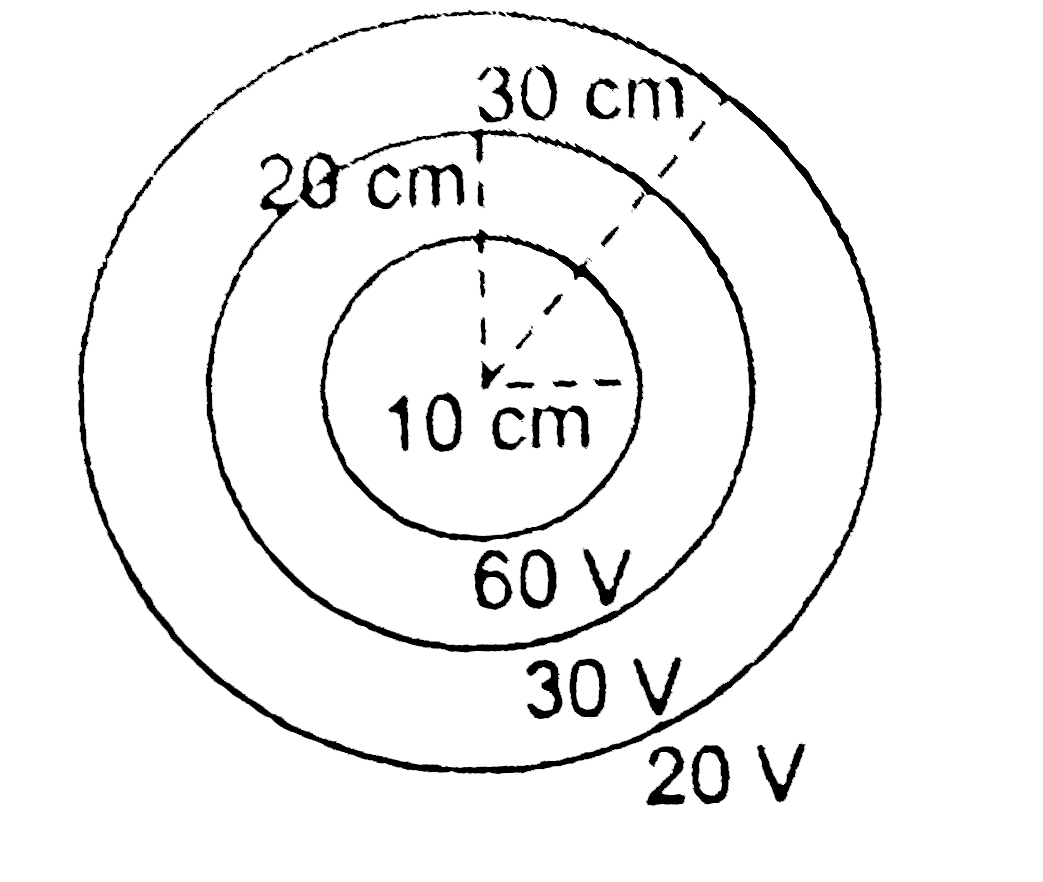
View SolutionSome equi-potential surfaces are shown in figure. What can you say about the magnitude and the direction of the electric field ?
View SolutionEquilibrium OF charges||Intensity OF Electric Field
View SolutionA dielectric slab of material having dielectric constant 6 is kept inside the electric field of magnitude E. What will be the net electric field intensity inside it?
View SolutionA metal slab is placed in a uniform electric field →E. What will be the net electric field intensity inside it?
View SolutionSome equipotential surfaces are shown in the figure below, what can you say about the magnitude and the direction of the electric field ?

View Solution