Assertion : Half of the ring is uniformly positively charged and other half uniformly negatively charged. Then, electric field is zero at centre. Then , electric field is zero at centre.

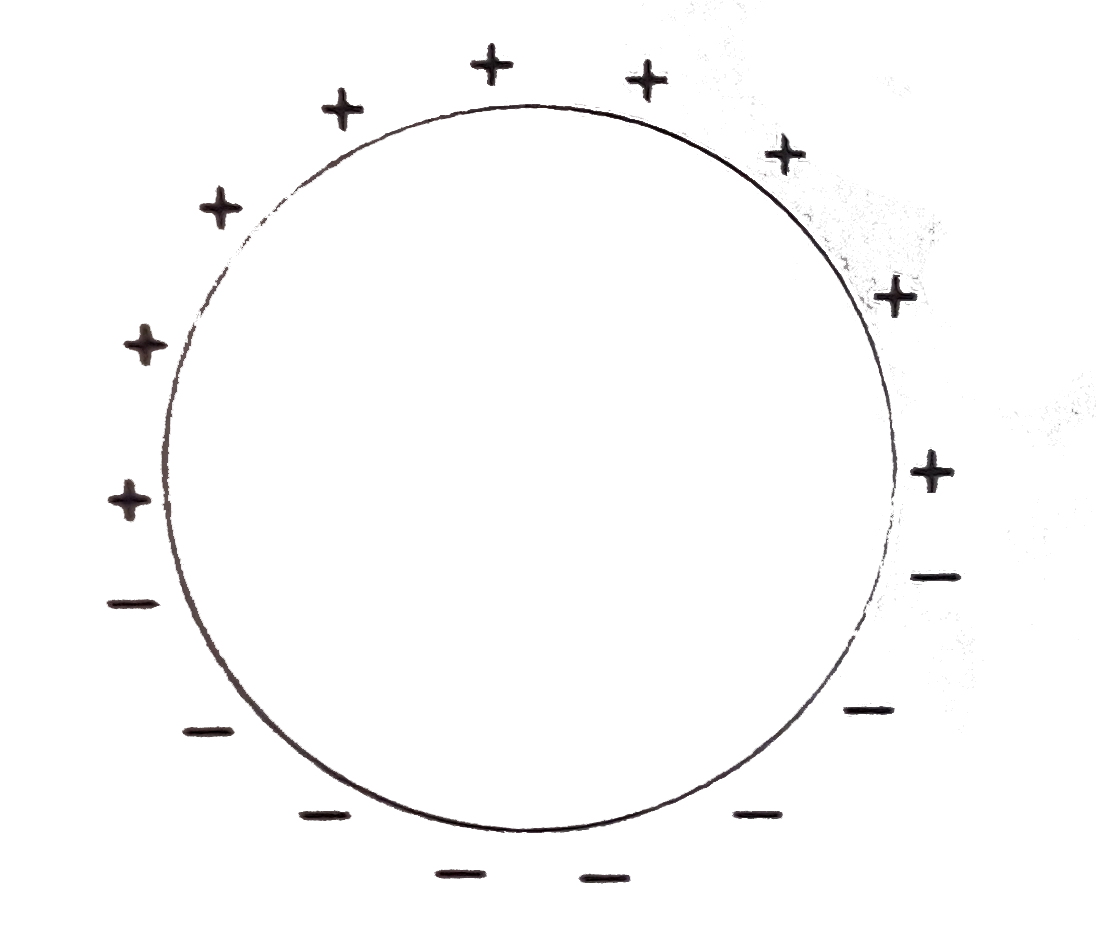
Reason : At the centre of uniformly charged ring, electric field is zero.

Video Solution

Text Solution

Verified by Experts

If we select two identical small segments of the ring that lie at the two ends of diameter of the ring, then electric field of these two segments will cancel cach other. And in the same way we can understand that electric field will be zero due to complete ring

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Assertion : The field strength at the centre of a ring is zero
Reason : At the centre of the ring, slope of V-r graph is zero.\
AIf both Assertin and Reason are correct and Reason is the correct explanation of Assertion
BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
CIf Assertion is true but Reason is false
DIf Assertion is false but Reason is true
Question 2 - Select One
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
A $\frac{1}{4 π ε_{0}} \frac{q}{3 \sqrt{3} R^{2}}$
B $\frac{1}{4 π ε_{0}} \frac{2 q}{3 R^{2}}$
C $\frac{1}{4 π ε_{0}} \frac{2 q}{3 \sqrt{3} R^{2}}$
D $\frac{1}{4 π ε_{0}} \frac{3 q}{2 \sqrt{2} R^{2}}$
Question 3 - Select One
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
Adecreases as r increases for $r < R$ and $r > R$
Bincreases as r increases for $r < R$ and $r > R$
Czero as r increases for $r < R$ , decreases as r increases for $r > R$
Dzero as r increases for $r < R$ , increases for $r > R$

MODERN PUBLICATION-ELECTRIC CHARGES AND FIELDS -Conceptual Questions

Home
Ask Doubt
Profile