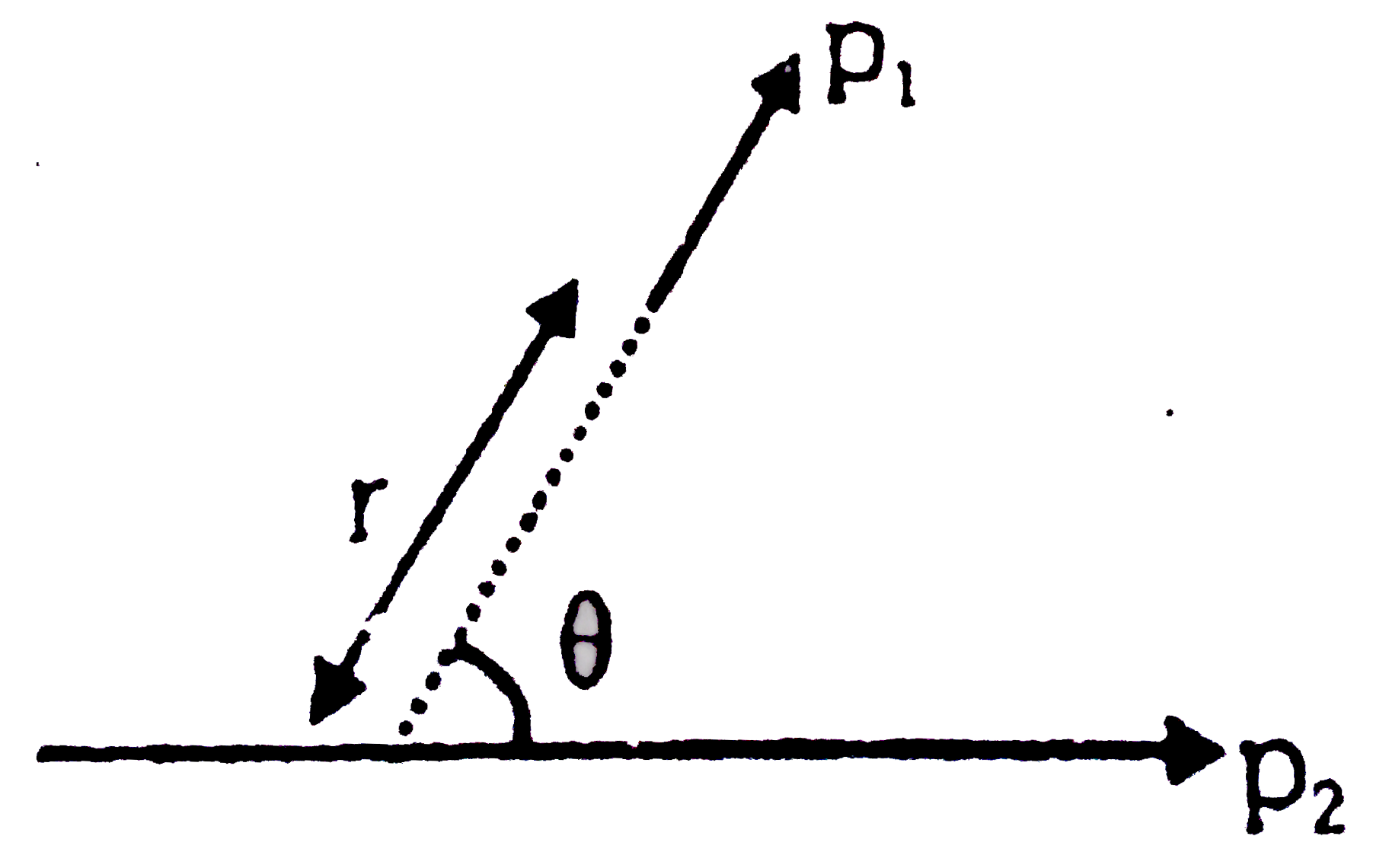
Two short electric dipoles are placed in such a manner that their axis coincides and distance between their centres is r. Electric force between these two shart dipoles is found to be proportional r−n. What will be the value of n?

Text Solution
The correct Answer is:4
Electric field on the axis of a short dipole is E=14πε02pr3, Force on an electric dipole placed in electric field which is changing along the axis of dipole is given by F=pdEdr .
We can write force between electric dipoles in the given situations as follows :
F=p1ddr[14πε02p2r3]
⇒F=2p1p24πε0ddr[1r3]=2p1p24πε0(−3r4)
⇒|F|=6p1p24πε0(r−4)
We can write on comparing that n =4 .
|
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (Matrix))
2 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Knowledge Check
Two electric dipoles are placed in such a manner that their electric dipole moments are directed towards each other. The force between them will be
AattractiveBinversely proportional to the cube of distance between chargesCnversely proportional to the fourth power of the distance between chargesDzeroAn electric dipole in placed completely inside a sphere in such a manner that centre of dipole coincides with the centre of sphere.
AFlux of electric field through the sphere may be non-zero.BFlux of electric field through the sphere must be zero.CElectric field intensity everywhere on sphere is zero.DElectric field intensity everywhere on sphere is non-zeroThe electric field due to an extremely short dipole at distance r from it is proportional to :
A1rB1r2C1r3D1r4
Two short electric dipoles are placed as shown. The energy of electric interaction these dipoles will be
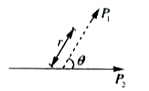
View SolutionTwo short electric dipoles are placed as shown in figure. Find the potential energy of electric interaction between these dipoles.
[−Kp1p2cosθr3]
View SolutionThe electric field due to an extremely short dipole at distance r from it is proportional to :
View SolutionThe electric field due to a dipole at a distance r from its centre is proportional to
View SolutionThe electric potential due to an extermely short dipole at a distance r form it is proporitonal to
View Solution