The magnitude of electric field intensity and electric potential due to a point charge at a point is 72 N/C and 36V, respectively. Calculate magnitude of the charge and distance of the point from point charge.
To solve the problem, we need to find the magnitude of the charge (Q) and the distance (R) from the point charge, given the electric field intensity (E) and electric potential (V).
1. Identify the given values:
- Electric field intensity, E=72N/C
- Electric potential, V=36V
2. Use the formulas for electric field and electric potential:
- The electric field E due to a point charge Q at a distance R is given by:
E=kQR2
- The electric potential V due to a point charge Q at a distance R is given by:
V=kQR
where k is Coulomb's constant, k≈9×109N m2/C2.
3. Relate the two equations:
- From the equations for E and V, we can express E in terms of V and R:
E=VR
- Rearranging gives:
R=VE
4. Calculate the distance R:
- Substitute the values of V and E:
R=36V72N/C=0.5m
5. Substitute R back to find Q:
- Now, we can use either the equation for E or V to find Q. Let's use the potential equation:
V=kQR
- Rearranging gives:
Q=VRk
- Substitute V=36V, R=0.5m, and k=9×109N m2/C2:
Q=36×0.59×109=189×109=2×10−9C
6. Convert Q to nanocoulombs:
- Since 1nC=10−9C:
Q=2nC
Final Results:
- The magnitude of the charge Q is 2nC.
- The distance R from the point charge is 0.5m.
- Electric field intensity, E=72N/C
- Electric potential, V=36V
- The electric field E due to a point charge Q at a distance R is given by:
E=kQR2
- The electric potential V due to a point charge Q at a distance R is given by:
V=kQR
where k is Coulomb's constant, k≈9×109N m2/C2.
- From the equations for E and V, we can express E in terms of V and R:
E=VR
- Rearranging gives:
R=VE
- Substitute the values of V and E:
R=36V72N/C=0.5m
- Now, we can use either the equation for E or V to find Q. Let's use the potential equation:
V=kQR
- Rearranging gives:
Q=VRk
- Substitute V=36V, R=0.5m, and k=9×109N m2/C2:
Q=36×0.59×109=189×109=2×10−9C
- Since 1nC=10−9C:
Q=2nC
- The magnitude of the charge Q is 2nC.
- The distance R from the point charge is 0.5m.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 110videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 221videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
Electric field intensity at point P due to charge distributed over a sphere is:
 AE=14πε0qrBE=σR2ε0r2CE=14πε0qrDE=0
AE=14πε0qrBE=σR2ε0r2CE=14πε0qrDE=0
The magnitude of electric field intensity and potential at a point A due to a charge Q placed at point B are 25NC−1and35JC−1, respectively. Calculate the value of Q and distance between A and B.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionAt s point due to a point charge, the values of electric field intensity and potential are 32NC−1 and 16JC−1, respectively. Calculate the
a. magnitude of the charge, and
b. distance of the charge from the point of observation.View Solution" Electric field intensity due to a point charge " "q" ' at a distance 'r' from it is "
View SolutionElectric field intensity at point P due to charge distributed over a sphere is:
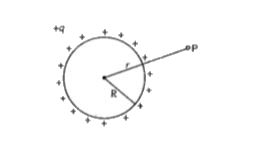 View Solution
View SolutionThe electric field due to a point charge at a distance 6 m from it is 630 N/C. The magnitude of the charge is
View SolutionThe magnitude of electric field intensity due to a point charge is 10 N/C at a distance 1 m from it. Calculate the magnitude of charge.
View Solution

