Electric field intensity in a region of space is given by →E=10x2ˆiN/C. What will be potential difference between point A(2, 5) and B(-1, 10)?
To find the potential difference between points A(2, 5) and B(-1, 10) in an electric field given by →E=10x2^i N/C, we will follow these steps:
Step 1: Understand the relationship between electric field and potential difference
The potential difference V between two points A and B in an electric field is given by the negative integral of the electric field along the path from A to B:
VAB=−∫BA→E⋅d→l
where d→l is the differential displacement vector along the path.
Step 2: Define the path of integration
Since the electric field is only in the x-direction, we can choose a path that moves only in the x-direction. The displacement vector can be defined as:
d→l=dx^i
where dx is the change in the x-coordinate.
Step 3: Substitute the electric field and displacement into the integral
The electric field →E=10x2^i and the displacement d→l=dx^i. Therefore, the dot product →E⋅d→l becomes:
→E⋅d→l=(10x2)(dx)
Step 4: Set up the integral for potential difference
Now we can set up the integral for the potential difference:
VAB=−∫xBxA10x2dx
where xA=2 and xB=−1.
Step 5: Evaluate the integral
Now we can evaluate the integral:
VAB=−∫−1210x2dx
Calculating the integral:
=−10(x33)−12
=−10((−1)33−(2)33)
=−10(−13−83)
=−10(−93)
=−10(−3)
=30 Volts
Conclusion
The potential difference VAB between points A(2, 5) and B(-1, 10) is 30 Volts.
---
The potential difference V between two points A and B in an electric field is given by the negative integral of the electric field along the path from A to B:
VAB=−∫BA→E⋅d→l
where d→l is the differential displacement vector along the path.
Since the electric field is only in the x-direction, we can choose a path that moves only in the x-direction. The displacement vector can be defined as:
d→l=dx^i
where dx is the change in the x-coordinate.
The electric field →E=10x2^i and the displacement d→l=dx^i. Therefore, the dot product →E⋅d→l becomes:
→E⋅d→l=(10x2)(dx)
Now we can set up the integral for the potential difference:
VAB=−∫xBxA10x2dx
where xA=2 and xB=−1.
Now we can evaluate the integral:
VAB=−∫−1210x2dx
Calculating the integral:
=−10(x33)−12
=−10((−1)33−(2)33)
=−10(−13−83)
=−10(−93)
=−10(−3)
=30 Volts
The potential difference VAB between points A(2, 5) and B(-1, 10) is 30 Volts.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 1
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 2
21 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Knowledge Check
If the electric field is given by →E=(100x2)i the potential difference between points x=10m and x=20m in volts is
A−5B5C−10D10Electric field at a distance x from the origin is given as E=100N−m2/Cx2 . Then potential difference between the points situated at x = 10 m and x = 20m is :-
A5 VB10 VC15 VD4VThe electric field intensity at all points in space is given by →E=√3ˆi−ˆj volts//metre. The nature of equipotential lines is x-y plane is given by
A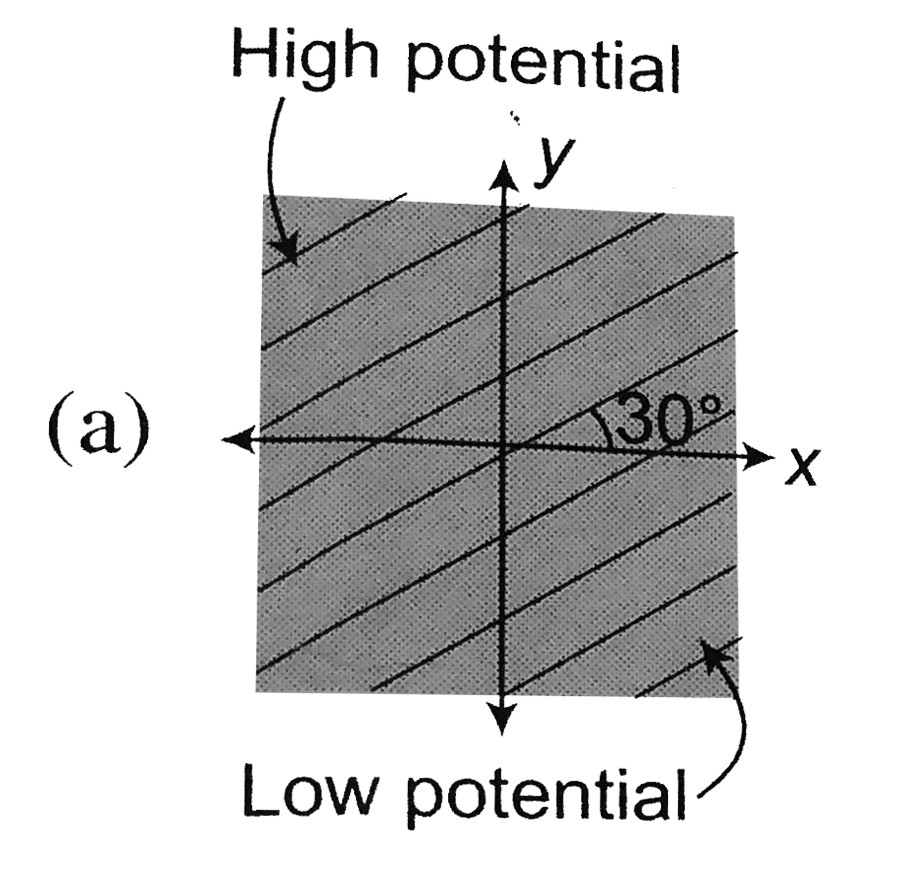
B
C
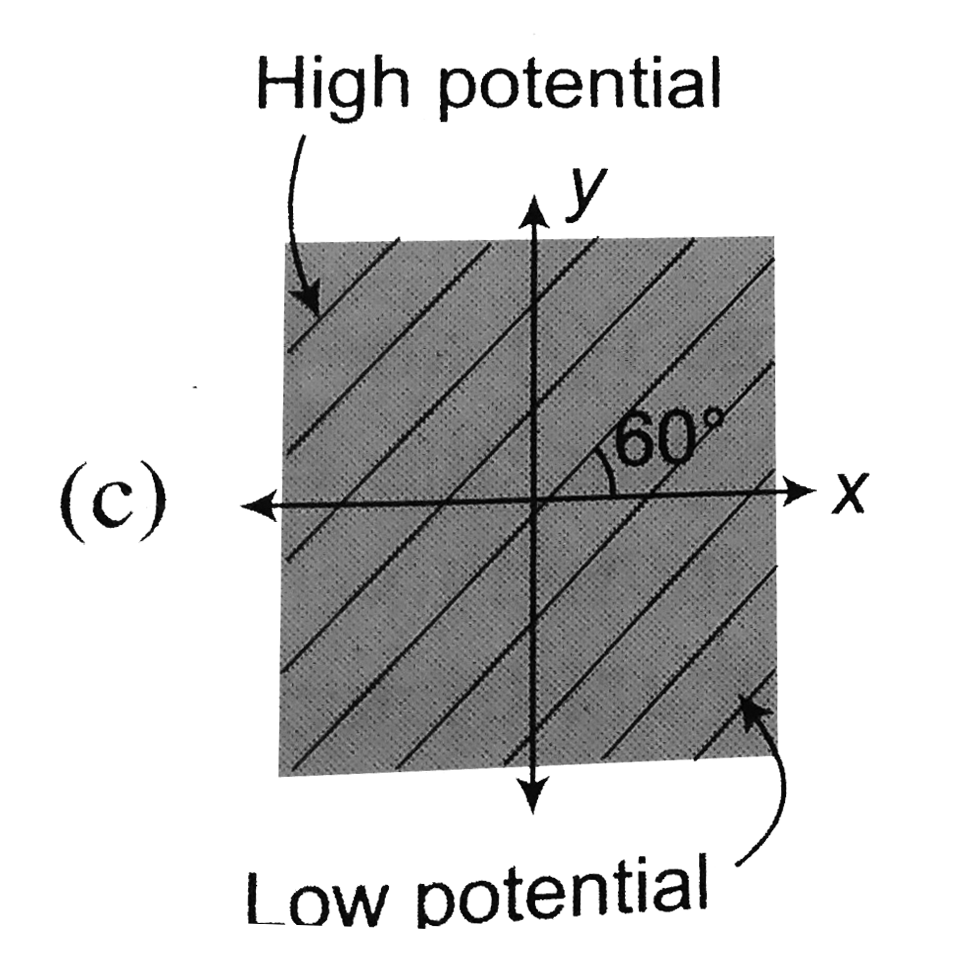D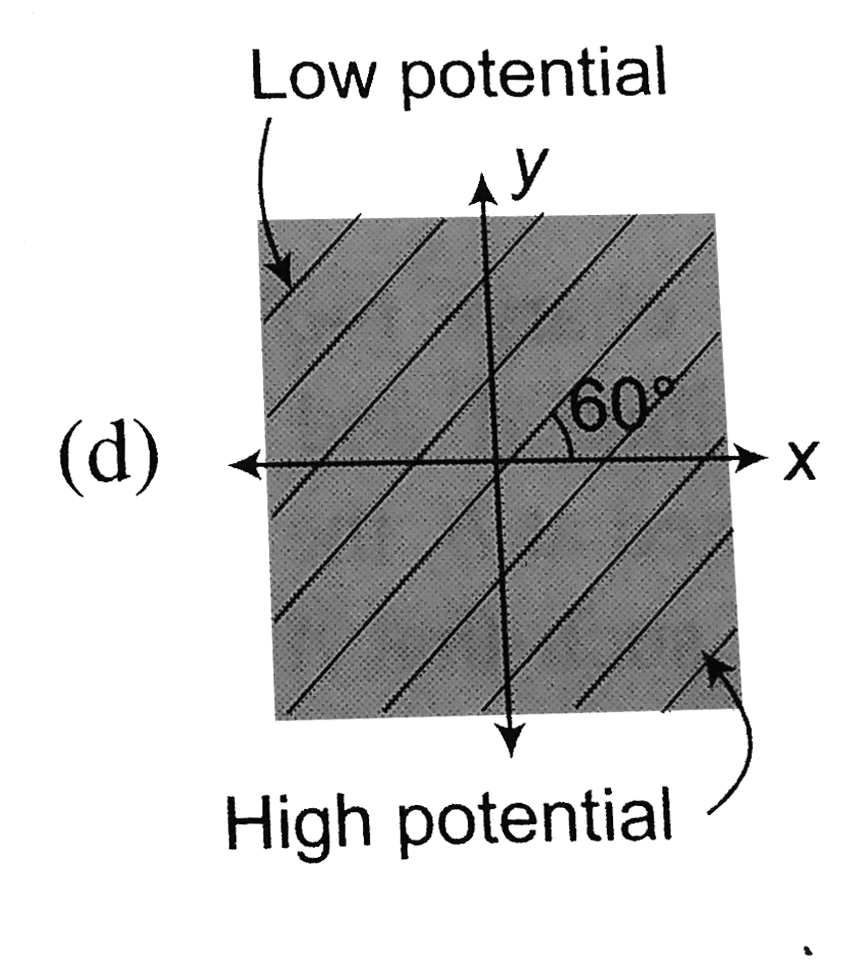
Electric potential in a region of space is given by V=(x2+y2+z2)V. What will be electric field intensity at a point P(-1m, 2m, -3m)?
View SolutionElectric field intensity in a region of space is given by →E=4ˆi+6ˆj+3ˆk N/C. Consider a plane surface of area 10 units parallel to Y-Z plane and calculate electric flux linked through this surface.
View SolutionThree points A,B,C lie in a uniform electric field E of 5×103N/C as shown in Fig. Find the potential difference between A and C.
View SolutionThe electric field in a certain region is given by E=5ˆi−3ˆjkv/m. The potential difference VB−VA between points a and B having coordinates (4, 0, 3) m and (10, 3, 0) m respectively, is equal to
View SolutionThe electric field in a region of space is given by E=5ˆi+2ˆjN/C. The flux of E due ot this field through an area 1m2lying in the y-z plane, in SI units is
View Solution