A charge of 108 μC is given to a metallic spherical shell of radius1 m. (i) Calculate electric potential at the surface of the shell. (ii) Calculate electric potential at a point that is 0.1 m from the centre of the shell.
To solve the problem, we will follow these steps:
Given Data:
- Charge, Q=108μC=108×10−6C=1.08×10−4C
- Radius of the spherical shell, R=1m
(i) Calculate electric potential at the surface of the shell.
1. Formula for Electric Potential: The electric potential V at the surface of a charged spherical shell is given by the formula:
V=kQR
where k=14πϵ0≈9×109N m2/C2.
2. Substituting the Values:
V=(9×109)×(1.08×10−4)1
3. Calculating:
V=9×109×1.08×10−4=972000V=9.72×105V
(ii) Calculate electric potential at a point that is 0.1 m from the center of the shell.
1. Understanding Electric Potential Inside the Shell: Inside a metallic spherical shell, the electric field is zero. Therefore, the electric potential inside the shell is constant and equal to the potential at the surface.
2. Using the Result from Part (i):
Vinside=Vsurface=9.72×105V
Final Answers:
- (i) Electric potential at the surface of the shell: V=9.72×105V
- (ii) Electric potential at a point that is 0.1 m from the center of the shell: V=9.72×105V
- Charge, Q=108μC=108×10−6C=1.08×10−4C
- Radius of the spherical shell, R=1m
V=kQR
where k=14πϵ0≈9×109N m2/C2.
V=(9×109)×(1.08×10−4)1
V=9×109×1.08×10−4=972000V=9.72×105V
Vinside=Vsurface=9.72×105V
- (i) Electric potential at the surface of the shell: V=9.72×105V
- (ii) Electric potential at a point that is 0.1 m from the center of the shell: V=9.72×105V
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 110videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 221videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Charge of 12μC is given toa hollow metallic sphere of radius 0.1 m. find the potential at (i) the surface of the sphere (ii) the centre of the sphere.
View SolutionBoth question (33) and (34) refer to the system of charges as shown in the figure. A spherical shell with an inner radius 'a' and an outer radius 'b' is made of conducting material. A point charge +Q is placed at the centre of the spherical shell and a total charge -q is placed on the shell.
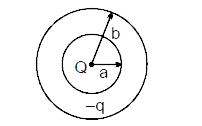
Assume that the electrostatic potential is zero at an infinite distance from the spherical shell. The electrostatic potential at a distance R(a<R<b) from the centre of the shell isView Solution
Knowledge Check
- Question 1 - Select One
A thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
A(a) 2Q4πε0RB(b) 2Q4πε0R−2q4πε0RC(c) 2Q4πε0R+q4πε0RD(d) (q+Q)24πε0R - Question 2 - Select One
A body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
A−GH(M+m)B−GH(M−m)C−GH(mMM+m)D−GH(mMM−m) - Question 3 - Select One
A spherical shell of radius R has a charge +q units. The electric field due to the shell at a point
Ainside is zero and varies as r−1 outside itBinside is constant and varies as r−2Cinside is zero and varies as r−2 outside itDinside is constant and varies as r−1 outside it
A point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionFind the electric potential energy of a unifomly charged then spherical shell.
View SolutionA particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R from the center of the shell. Find the electric potential at the center of the shell.
View Solution

