A capacitor of capacitance C is found to store a charge 480 μC when it is connected across a battery of potential difference V. Charge stored in the capacitor becomes 160μC when potential difference is reduced by 160V. Calculate C and V.
To solve the problem step by step, we will use the relationships between charge (Q), capacitance (C), and potential difference (V).
Step 1: Write down the first equation using the initial conditions.
The charge stored in a capacitor is given by the formula:
Q=C×V
From the problem, we know that when the capacitor stores a charge of Q=480μC, we can write:
480μC=C×V(Equation 1)
Step 2: Write down the second equation using the new conditions.
When the potential difference is reduced by 160V, the new potential difference becomes V−160V, and the charge stored is now Q=160μC. Thus, we can write:
160μC=C×(V−160)(Equation 2)
Step 3: Set up the equations for solving.
Now we have two equations:
1. 480=C×V
2. 160=C×(V−160)
Step 4: Solve Equation 1 for C.
From Equation 1, we can express C in terms of V:
C=480μCV(Equation 3)
Step 5: Substitute Equation 3 into Equation 2.
Substituting Equation 3 into Equation 2:
160=(480V)×(V−160)
Step 6: Simplify and solve for V.
Multiply both sides by V:
160V=480(V−160)
Expanding the right side:
160V=480V−76800
Rearranging gives:
480V−160V=76800
320V=76800
Dividing both sides by 320:
V=76800320=240V
Step 7: Substitute V back to find C.
Now that we have V, we can substitute it back into Equation 3 to find C:
C=480μC240V=2μF
Final Result:
Thus, the values of capacitance and potential difference are:
C=2μFandV=240V
---
Q=C×V
From the problem, we know that when the capacitor stores a charge of Q=480μC, we can write:
480μC=C×V(Equation 1)
160μC=C×(V−160)(Equation 2)
1. 480=C×V
2. 160=C×(V−160)
C=480μCV(Equation 3)
160=(480V)×(V−160)
160V=480(V−160)
Expanding the right side:
160V=480V−76800
Rearranging gives:
480V−160V=76800
320V=76800
Dividing both sides by 320:
V=76800320=240V
C=480μC240V=2μF
C=2μFandV=240V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 1
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 2
21 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Knowledge Check
A capacitor of capacitance C is connected across a battery of potential difference V. The energy stored in the capacitor is 12CV2
The energy supplied by the battery is 12CV2.ABoth A and R falseBBoth A and R true and R is not correct reason for ACA is true and R is falseDBoth A and R are true and R is correct reason of A.A capacitor of capacitance 500μF is charged at the rate of 100μC/s. The time in which the potential difference will become 20V, is :
A100sB50 sC20 sD10 sFind the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
A0.02JB0.04JC0.01JD0.05J
A capacitor is charged to a potential difference of 100V and then it is connected across a resistor.After one second,the potential drop across the plates of the capacitor becomes 80V .Then after 2sec the potential difference
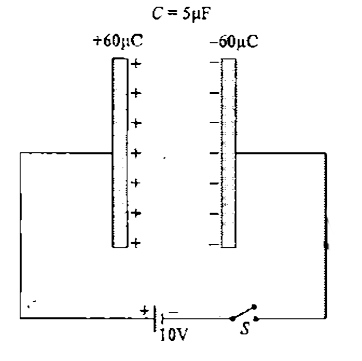
View SolutionA capacitor of 5μF capacitance is charged with an initial charge 60μC as shown in figure and connected across a 10Vbattery. Find the amount of heat produced when switch is closed.
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts . The charge stored in it is 360μC . When potential across the capacitor is reduced by 120 V , the charge stored in it becomes 120 μC . Calculate :
What will be the charge stored in the capacitor , if the voltage applied had increased by 120 V ?
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts . The charge stored in it is 360μC . When potential across the capacitor is reduced by 120 V , the charge stored in it becomes 120 μC . Calculate :
The potential V and the unknown capacitance C .
View SolutionTwo capacitors of capacitances 10μFand20μF are connected in series across a potential difference of 100V. The potential difference across each capacitor is respectively
View Solution
