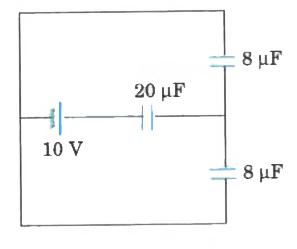
Find the charges stored in each of the capacitors shown in the circuit diagram.
Video Solution
Text Solution
This given arrangement can be simplified as below:

Equivalent capacitance of two 8 μF capacitors connected in parallel is
C=(8+8)μF=16μF
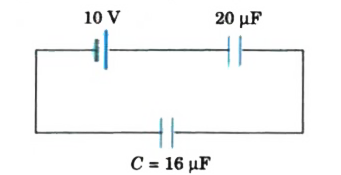
The net capacitance of the network, which are connected in series, is:
1Ceq=120+116
Ceq=20×1620+16=8.89μF
Charge drawn from the battery,
Q=CeqV
Here, V=10V
⇒Q=8.89×10−6×10
=88.9×10−6μC=88.9μC
Charge on capacitor of 20μF=Q=88.9μC
Charge on the two 8μF capacitors will be distributed equally.
Charge on each 8μF capacitor =Q2=44.45μC
|
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 1
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 2
21 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Knowledge Check
what is the charge stored on each capacitor C1andC2 in the circuit shown in fig.
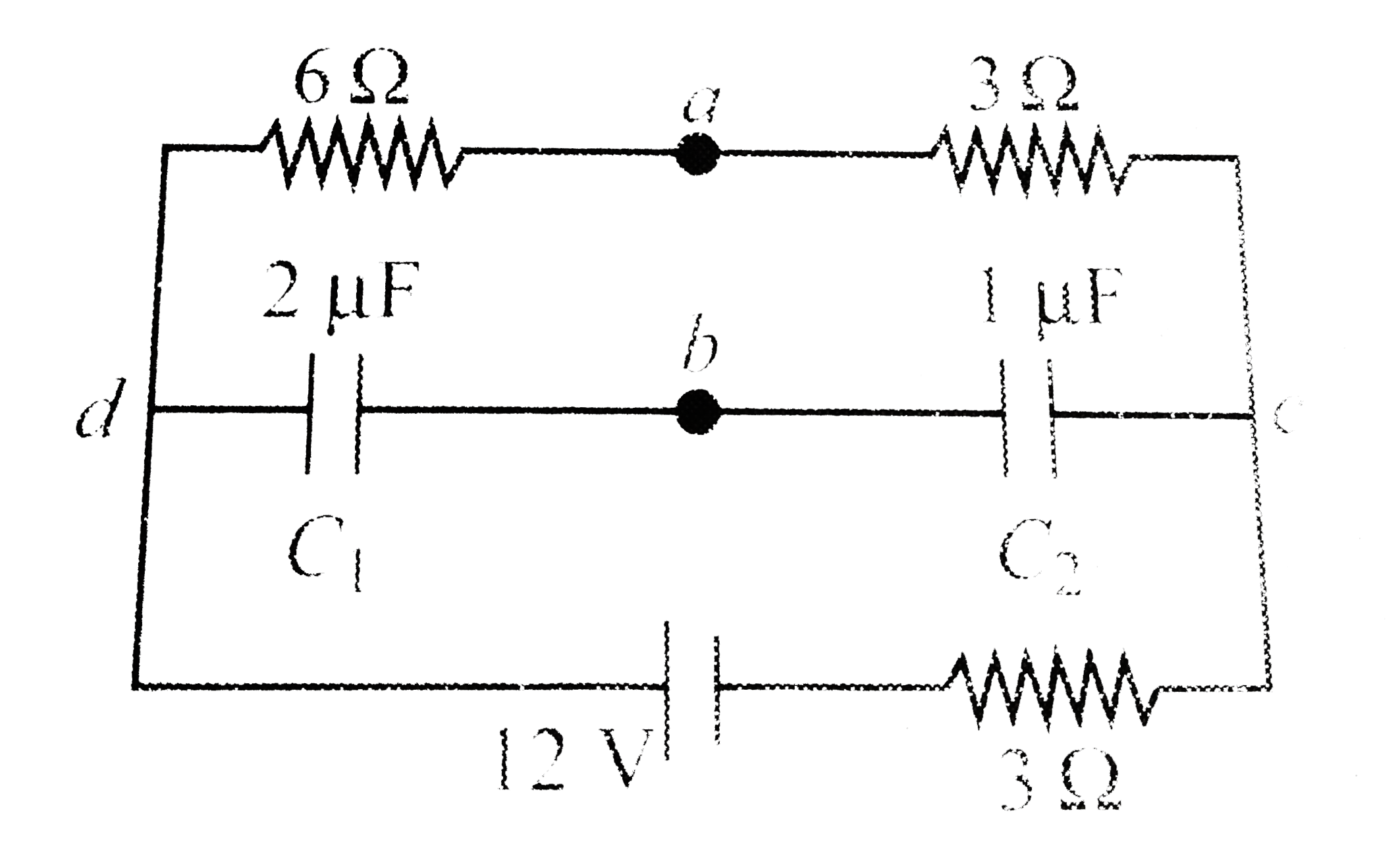 A6μC,6μCB6μC,3μCC3μC,6μCD3μC,3μC
A6μC,6μCB6μC,3μCC3μC,6μCD3μC,3μC
Find the charge stored in the capacitor.
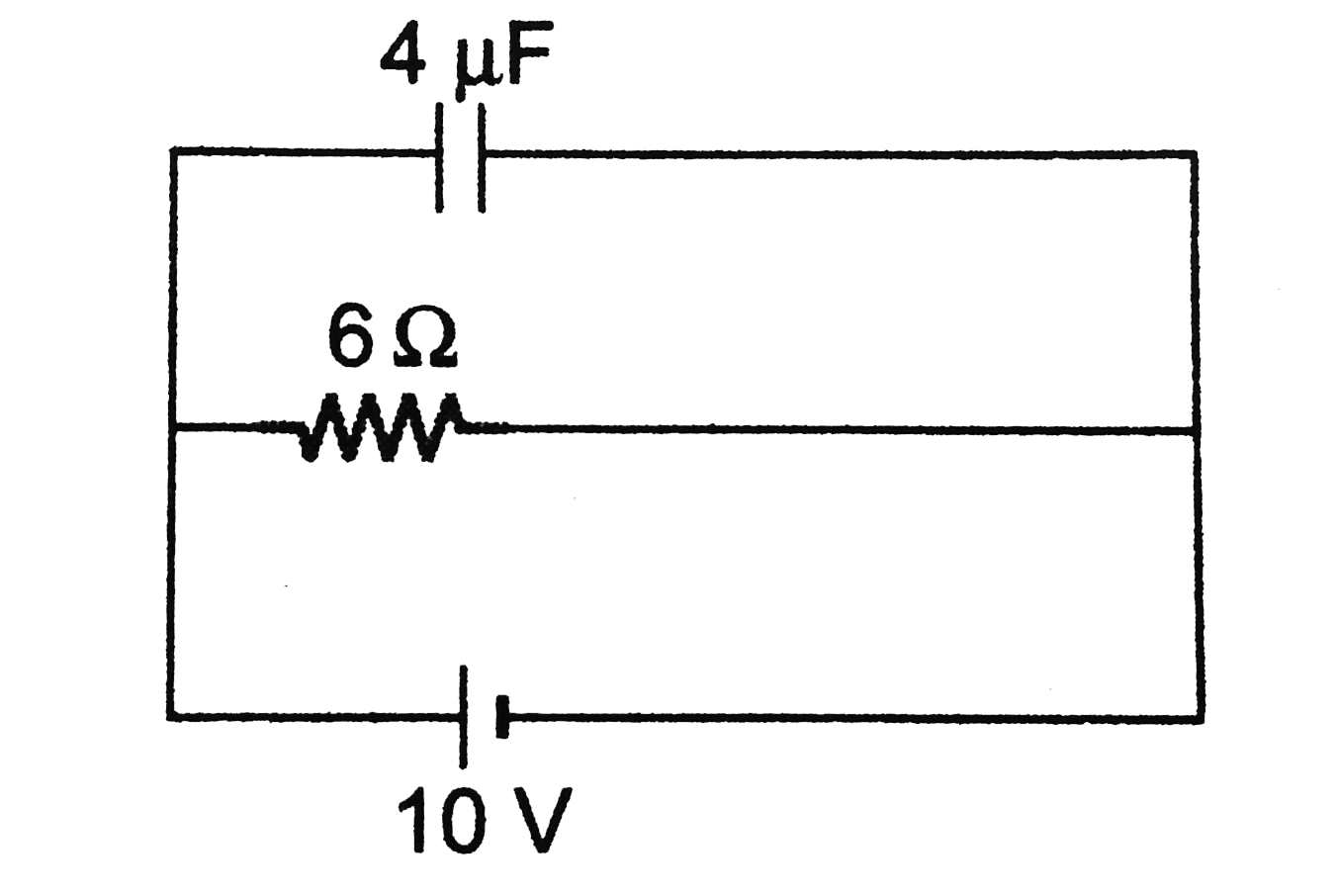
View SolutionFind the charge stored in the capacitor.
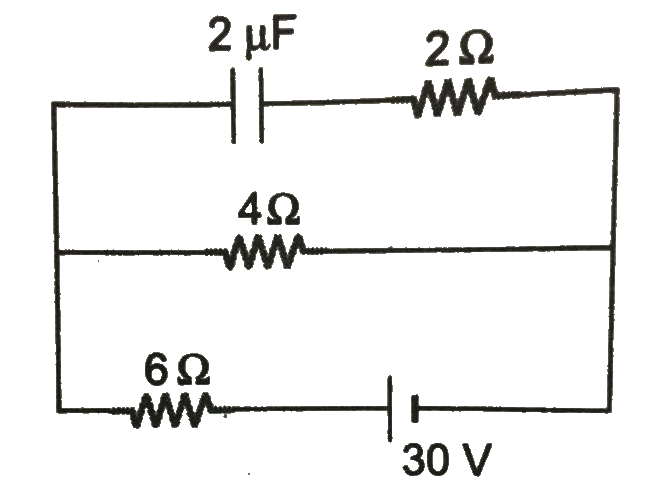
View SolutionFind the charge appearing on each of the three capacitors shown in Fig.
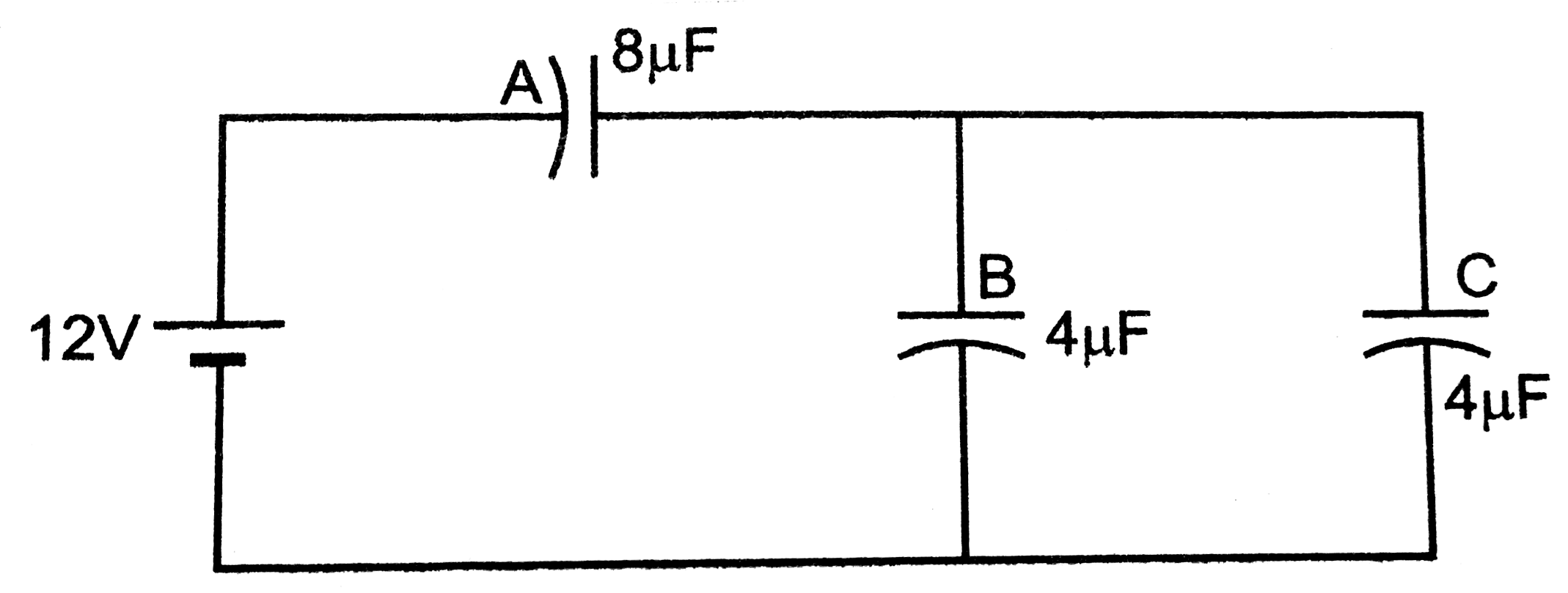
View SolutionFind the steady state charge stored in the capacitor.

View SolutionFind the steady state charge stored in the capacitor.
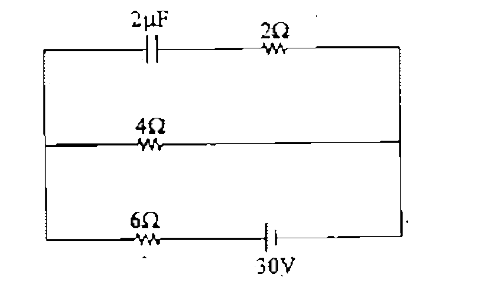
View SolutionFind the charge stored in the capacitor in steady state in the circuit shown below.

View SolutionFind the charge on the capacitor shown in figure
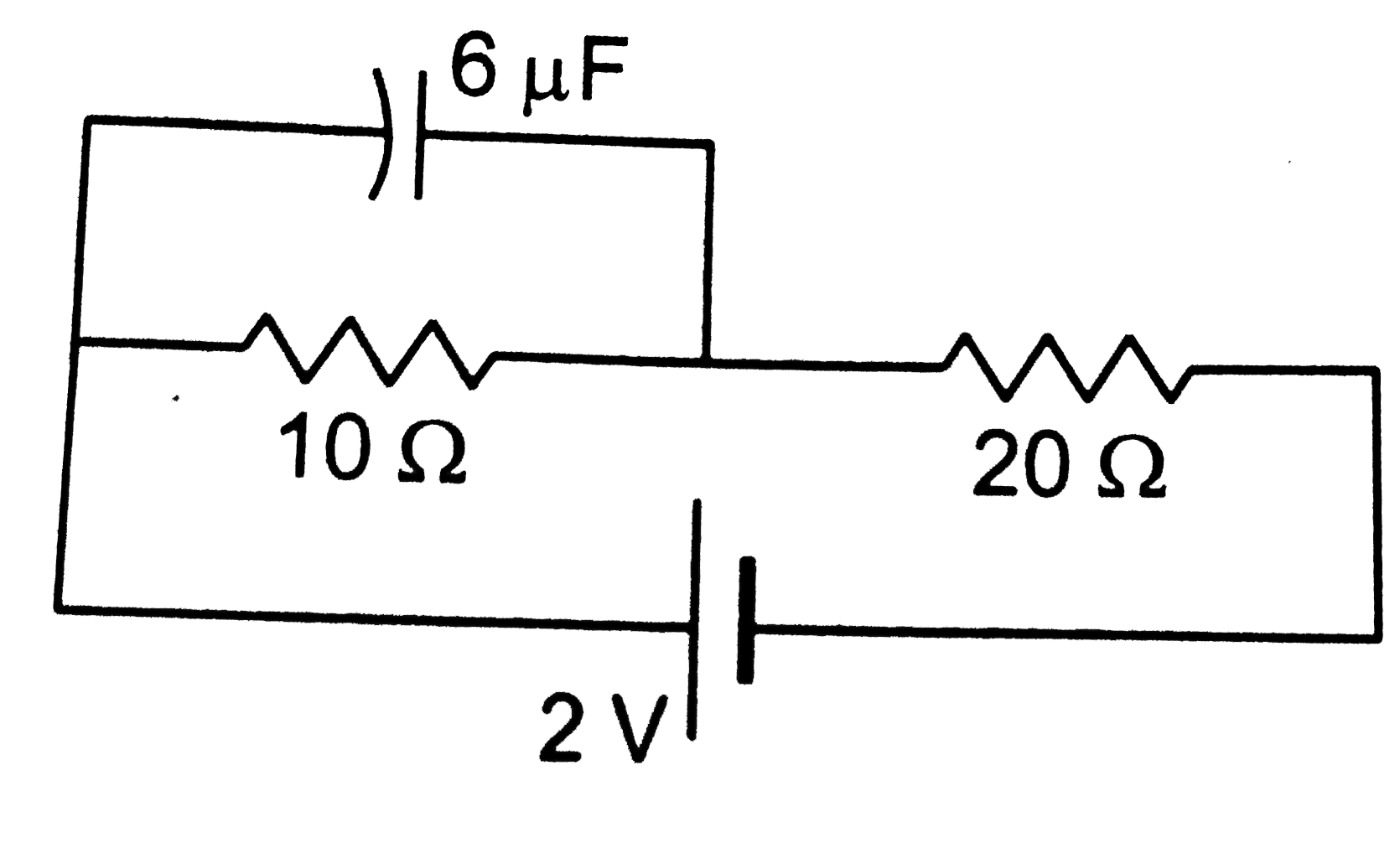
View Solution