A square with vertices A (0, 0), B (3 cm, 0), C (3 cm, 3 cm) and D (0, 3 cm) is placed in a region of electric field . Calculate the work done in slowly moving a charge of (i) From A to B (ii) From C to D.
To solve the problem, we need to calculate the work done in moving a charge of 0.1μC (which is 0.1×10−6C) in an electric field given by →E=(x+y)^i+2y^jV/m. We will calculate the work done for two cases: (i) moving from A to B and (ii) moving from C to D.
1. Identify the path from A to B:
- The coordinates of A are (0,0) and of B are (3cm,0).
- The movement is along the x-axis, so y=0 throughout the movement.
2. Express the differential displacement:
- The differential displacement vector d→s=dx^i.
3. Calculate the electric field along the path:
- Since y=0, the electric field becomes:
→E=(x+0)^i+2(0)^j=x^i
4. Calculate the work done by the electric field:
- The work done dW by the electric field is given by:
dW=q→E⋅d→s=qExdx
- Substituting the values:
dW=(0.1×10−6)(x)dx
5. Integrate from A to B:
- The limits of integration for x are from 0 to 3cm=0.03m:
W=∫0.030(0.1×10−6)xdx
- Calculating the integral:
W=(0.1×10−6)(x22)0.030=(0.1×10−6)((0.03)22)
=(0.1×10−6)(0.00092)=(0.1×10−6)×0.00045=4.5×10−11J
6. Calculate the work done by external force:
- The work done by the external force is:
Wexternal=−W=−4.5×10−11J
Part (ii): Work Done from C to D
1. Identify the path from C to D:
- The coordinates of C are (3cm,3cm) and of D are (0,3cm).
- The movement is along the line where y=3cm=0.03m and x varies from 0.03m to 0.
2. Express the differential displacement:
- The differential displacement vector d→s=−dx^i.
3. Calculate the electric field along the path:
- Since y=0.03:
→E=(x+0.03)^i+2(0.03)^j=(x+0.03)^i+0.06^j
4. Calculate the work done by the electric field:
- The work done dW by the electric field is given by:
dW=q→E⋅d→s=q((x+0.03)(−dx))
- Substituting the values:
dW=−(0.1×10−6)(x+0.03)dx
5. Integrate from C to D:
- The limits of integration for x are from 0.03 to 0:
W=−∫00.03(0.1×10−6)(x+0.03)dx
- This can be rewritten as:
W=(0.1×10−6)∫0.030(x+0.03)dx
- Calculating the integral:
W=(0.1×10−6)(x22+0.03x)0.030
=(0.1×10−6)((0.03)22+0.03(0.03))
=(0.1×10−6)(0.00045+0.0009)=(0.1×10−6)×0.00135=1.35×10−10J
6. Calculate the work done by external force:
- The work done by the external force is:
Wexternal=−W=−1.35×10−10J
Final Answers:
- (i) Work done from A to B: −4.5×10−11J
- (ii) Work done from C to D: −1.35×10−10J
- The coordinates of A are (0,0) and of B are (3cm,0).
- The movement is along the x-axis, so y=0 throughout the movement.
- The differential displacement vector d→s=dx^i.
- Since y=0, the electric field becomes:
→E=(x+0)^i+2(0)^j=x^i
- The work done dW by the electric field is given by:
dW=q→E⋅d→s=qExdx
- Substituting the values:
dW=(0.1×10−6)(x)dx
- The limits of integration for x are from 0 to 3cm=0.03m:
W=∫0.030(0.1×10−6)xdx
- Calculating the integral:
W=(0.1×10−6)(x22)0.030=(0.1×10−6)((0.03)22)
=(0.1×10−6)(0.00092)=(0.1×10−6)×0.00045=4.5×10−11J
- The work done by the external force is:
Wexternal=−W=−4.5×10−11J
- The coordinates of C are (3cm,3cm) and of D are (0,3cm).
- The movement is along the line where y=3cm=0.03m and x varies from 0.03m to 0.
- The differential displacement vector d→s=−dx^i.
- Since y=0.03:
→E=(x+0.03)^i+2(0.03)^j=(x+0.03)^i+0.06^j
- The work done dW by the electric field is given by:
dW=q→E⋅d→s=q((x+0.03)(−dx))
- Substituting the values:
dW=−(0.1×10−6)(x+0.03)dx
- The limits of integration for x are from 0.03 to 0:
W=−∫00.03(0.1×10−6)(x+0.03)dx
- This can be rewritten as:
W=(0.1×10−6)∫0.030(x+0.03)dx
- Calculating the integral:
W=(0.1×10−6)(x22+0.03x)0.030
=(0.1×10−6)((0.03)22+0.03(0.03))
=(0.1×10−6)(0.00045+0.0009)=(0.1×10−6)×0.00135=1.35×10−10J
- The work done by the external force is:
Wexternal=−W=−1.35×10−10J
- (i) Work done from A to B: −4.5×10−11J
- (ii) Work done from C to D: −1.35×10−10J
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 2
21 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 3
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Chapter Practice Test
9 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
A charge of 0.5 nC is placed at the centre of an equilateral triangle of side 10 cm, calculate the work done in bringing a charge of 0.1 nC from infinity to any vertices of the triangle.
View SolutionCalculate the work done by electric field in moving an electron from point A(0, 2 cm) to point B(5cm, 9cm) in a region of electric field →E=104ˆjVm−1
View SolutionShow that A(3, 2), B(0, 5), C(-3, 2) and D(0, -1) are the vertices of a square.
View SolutionShow that the points A(3, 5), B(6, 0), C(1, -3) and D(-2, 2) are the vertices of a square ABCD.
View SolutionShow that the points A(2,1),B(0,3),C(−2,1)andD(0,−1) are the vertices of a square.
View SolutionCalculate the work done in moving a 1μC charge from A (5cm, 1cm) to B (1cm, 5cm) in a region of electric field of magnitude 103NC−1 and directed along the line x=y−5.
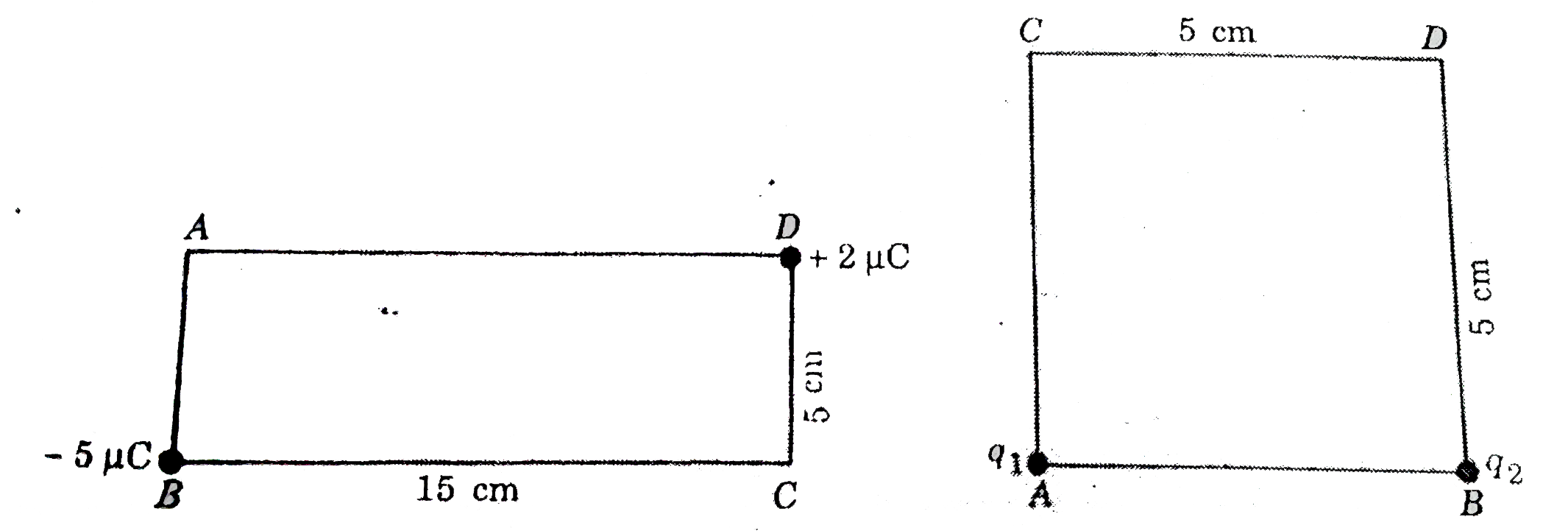
View SolutionThe sides of rectangle ABCD are 15 cm and 5 cm, as shown in figure. Point cahrges of −5μC and +2μC are placed at the vertices B and D respectively. Calculate electric potential at the vertices A and C. Also calculate the work done in carrying a charge of 3μC from A to C.
View SolutionCalculate the potential at point (0, 7 cm) due to a point charge of 0.2 μC placed at (0, 2 cm).
View SolutionA conducting square loop of side 10 cm is placed in a region of uniform magnetic field 0.5 T as shown in the figure. Calculate the work done in slowly moving the loop out of the field in 2 seconds with a speed of 0.05ms−1. The resistance of loop is 10 Ω.

View SolutionA 0.6 C of charge is placed at right angled vertex B of a right angle triangle. Calculate the potential at point A and C, if AB = 3 cm and BC = 4 cm. Also calculate the work done in slowly moving a -0.1 μC charge from point A to C.
View Solution
