Four point charges, +0.2μC,+0.2μC,−0.2μCand−0.2μC are placed on vertices A, B, C and D, respectively of square ABCD of side a. Calculate the electric potential at the centre of the square.
To calculate the electric potential at the center of the square formed by the four point charges, we can follow these steps:
Step 1: Identify the Charges and Their Positions
We have four charges:
- Charge at vertex A: Q1=+0.2μC
- Charge at vertex B: Q2=+0.2μC
- Charge at vertex C: Q3=−0.2μC
- Charge at vertex D: Q4=−0.2μC
These charges are placed at the vertices of square ABCD.
Step 2: Determine the Distance from the Center to Each Charge
The distance from the center of the square to any vertex can be calculated using the Pythagorean theorem. For a square of side length a, the distance r from the center to a vertex is given by:
r=a√2
Step 3: Calculate the Electric Potential Due to Each Charge
The electric potential V at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant (k≈8.99×109Nm2/C2).
For each charge at the center:
- For Q1 and Q2 (positive charges):
VA=kQ1r=k0.2×10−6a√2=0.2√2ka(for both Q1 and Q2)
Thus, the total potential due to both positive charges:
Vpositive=VA+VB=2⋅0.2√2ka=0.4√2ka
- For Q3 and Q4 (negative charges):
VC=kQ3r=k−0.2×10−6a√2=−0.2√2ka(for both Q3 and Q4)
Thus, the total potential due to both negative charges:
Vnegative=VC+VD=2⋅(−0.2√2ka)=−0.4√2ka
Step 4: Calculate the Net Electric Potential at the Center
Now, we can find the net electric potential Vnet at the center by adding the contributions from all four charges:
Vnet=Vpositive+Vnegative=0.4√2ka−0.4√2ka=0
Conclusion
The electric potential at the center of the square is:
0V
We have four charges:
- Charge at vertex A: Q1=+0.2μC
- Charge at vertex B: Q2=+0.2μC
- Charge at vertex C: Q3=−0.2μC
- Charge at vertex D: Q4=−0.2μC
The distance from the center of the square to any vertex can be calculated using the Pythagorean theorem. For a square of side length a, the distance r from the center to a vertex is given by:
r=a√2
The electric potential V at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant (k≈8.99×109Nm2/C2).
- For Q1 and Q2 (positive charges):
VA=kQ1r=k0.2×10−6a√2=0.2√2ka(for both Q1 and Q2)
Thus, the total potential due to both positive charges:
Vpositive=VA+VB=2⋅0.2√2ka=0.4√2ka
VC=kQ3r=k−0.2×10−6a√2=−0.2√2ka(for both Q3 and Q4)
Thus, the total potential due to both negative charges:
Vnegative=VC+VD=2⋅(−0.2√2ka)=−0.4√2ka
Now, we can find the net electric potential Vnet at the center by adding the contributions from all four charges:
Vnet=Vpositive+Vnegative=0.4√2ka−0.4√2ka=0
The electric potential at the center of the square is:
0V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 3
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 4
7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 1
10 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Four point charges +1μC,+1μC,−1μCand−1μC are placed at the corners A,B,C and D of a square of each side 0.1 m (i) Calculate electric potential at the center O of the square (ii) If E is middle point of BC, what is work done in carrying an electron from O to E ?
View SolutionFour point charges of +1μc each are placed on the four corners of a square of side 1 m. Calculate the electric potential at the centre of the square.
View Solution
Knowledge Check
Four charges q1=1μC,q2=2μC,q3=−3μC and q4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
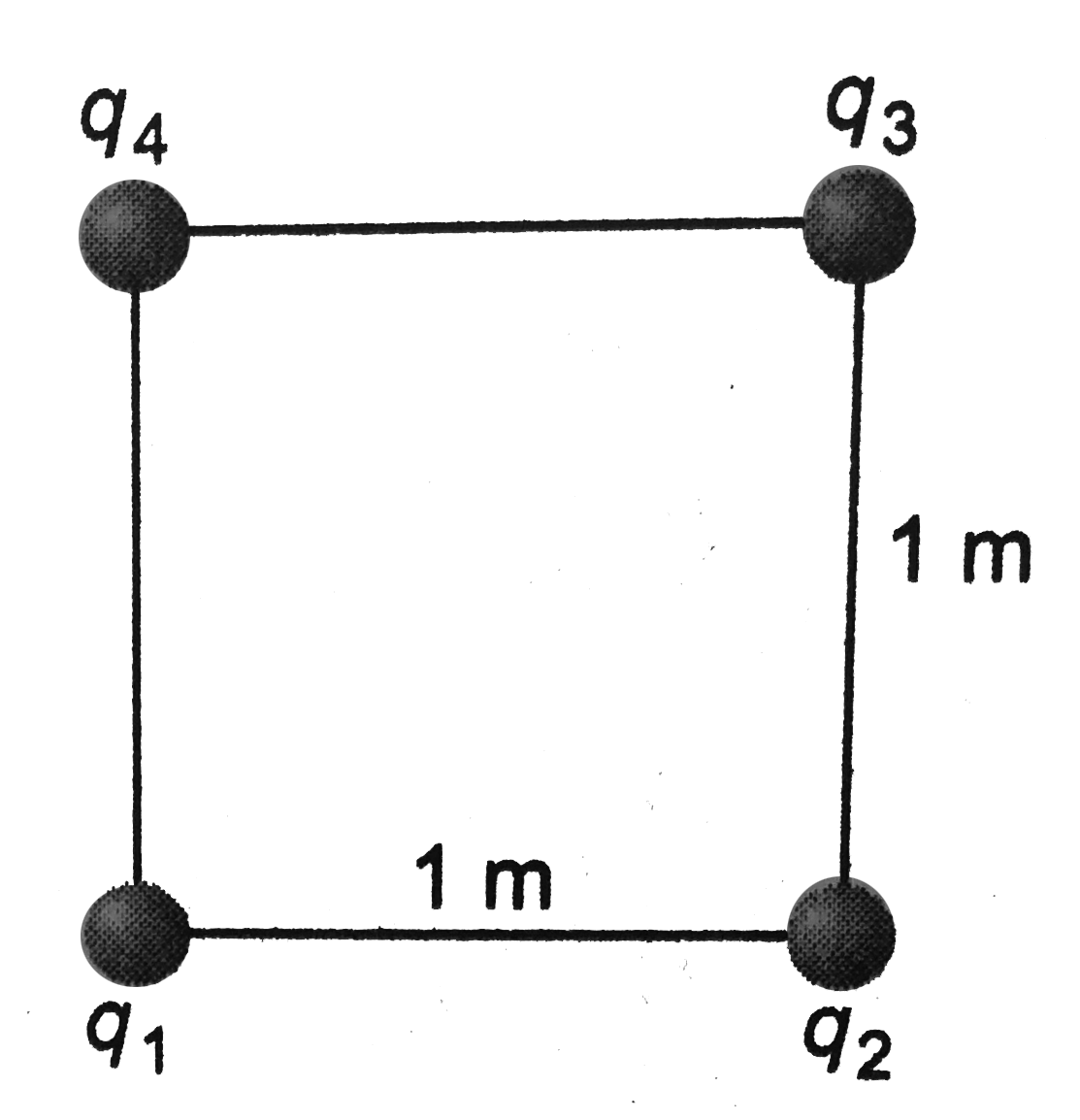 A−5.28×10−2JB−7.62×10−2JC−8.91×10−2JD−4.33×10−2J
A−5.28×10−2JB−7.62×10−2JC−8.91×10−2JD−4.33×10−2JElectric charge of 1μC,−1μC and 2μC are placed in air at the corners A, B and C respectively of an equilateral triangle ABC having length of each side 10 cm. The resultant force on the charge at C is
A0.9 NB1. 8NC2.7 ND3.6 NElectric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
A1.8 VB1.8×106VC1.8×105VD1.8×104V
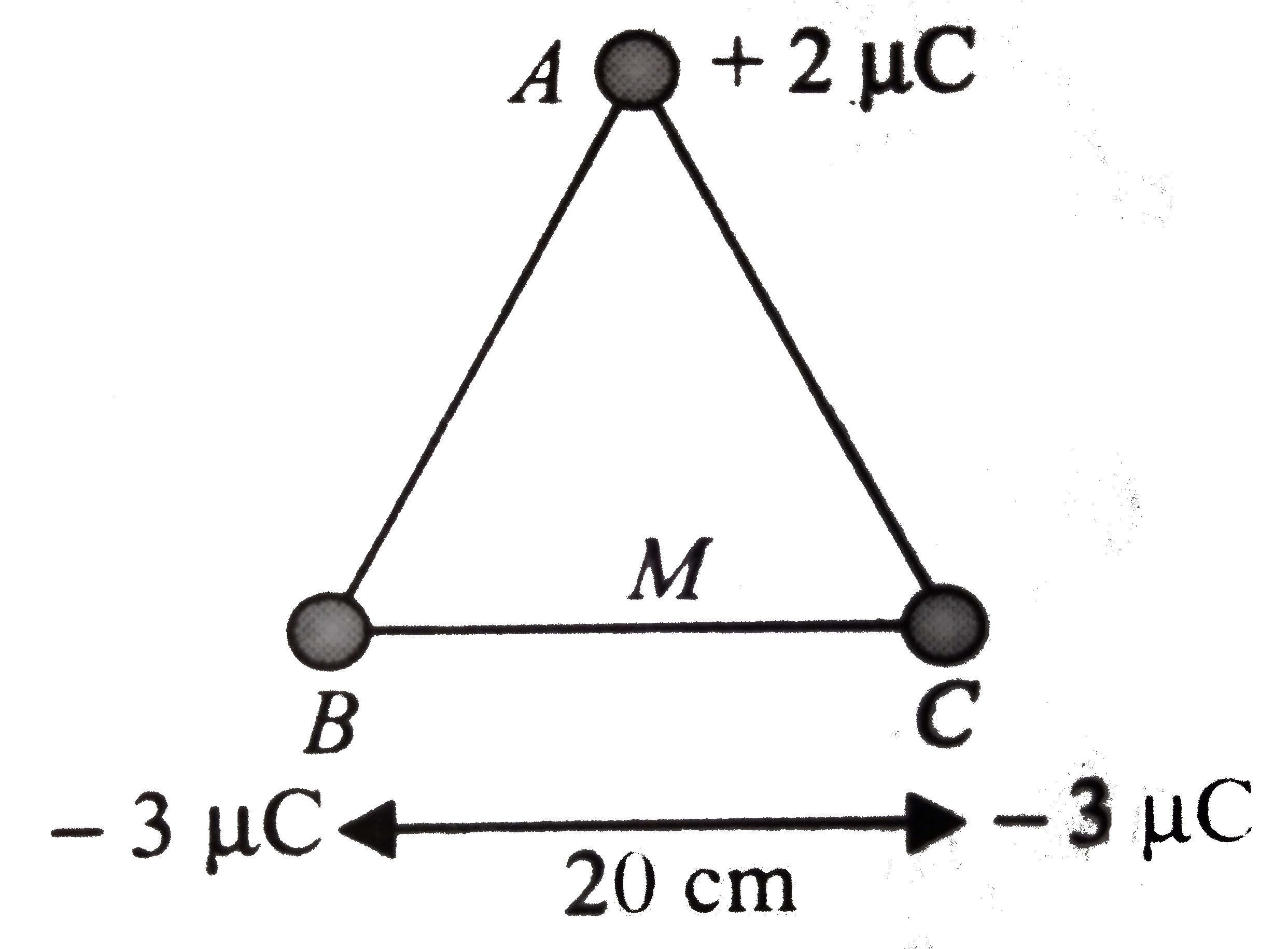
Three point charges of +2μC,−3μC , and −3μC are kept at the vertices A, B, and C, respectively of an equilatreral triangle of side 20 cm. what should be the sign and magnitude of the charge (q) to be placed at the midpoint (M) of side BC so that the charge at A remains in equilibrium?
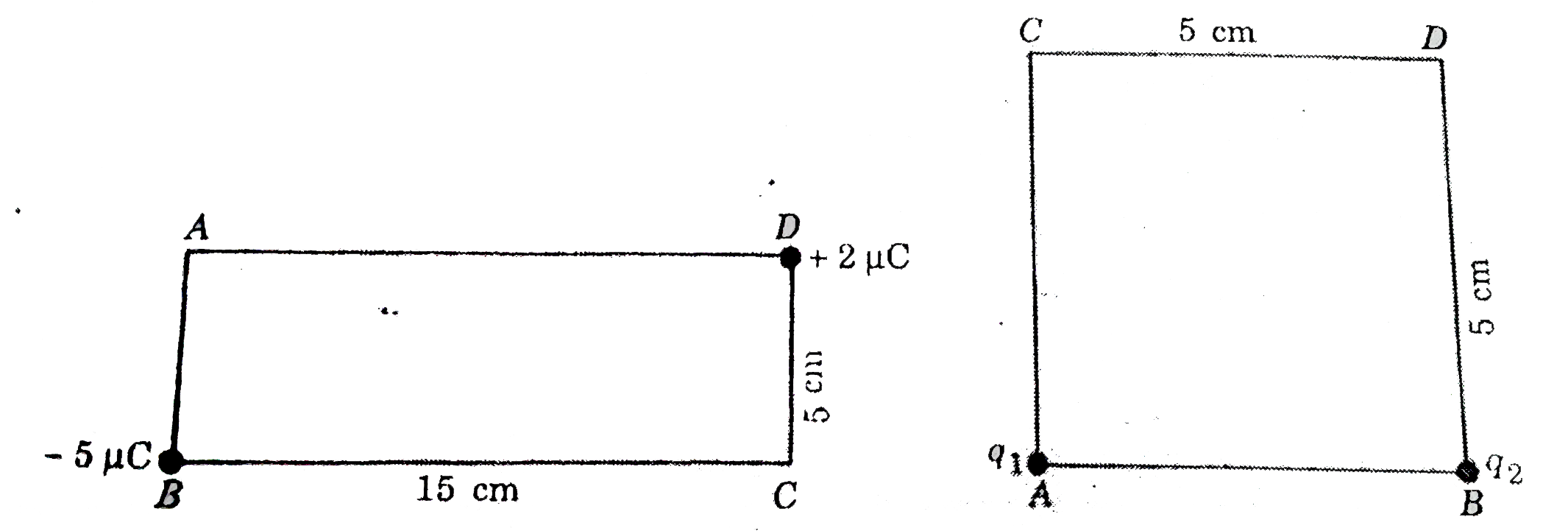
View SolutionThe sides of rectangle ABCD are 15 cm and 5 cm, as shown in figure. Point cahrges of −5μC and +2μC are placed at the vertices B and D respectively. Calculate electric potential at the vertices A and C. Also calculate the work done in carrying a charge of 3μC from A to C.
View SolutionThree charges −1μC,2μCand3νCare placed respectively at the corners A, B, C of an equiliateral triangle of sides 2m. Calculate the potential and electric field at the midpoint of the side BC.
View SolutionTwo point charges 8 μC and −8μC are kept at points (-2cm, 0) and (2cm, 0), respectively. Calculate the electric potential at points (0, 7cm) and (4cm, 0).
View SolutionFour charges qA=2μC,qB=−5μC,qc=2μC and qD=−5μC are placed at comers of a square ABCD of side 10 cm. What is the force on a charge of 1μC placed at centre of the square?
View Solution
