The charge stored in a capacitor of capacitance C, initially connected to a battery of V volts becomes half on reducing the potential difference across it by 100 V. Calculate the value of V.
To solve the problem step by step, we will use the relationship between charge, capacitance, and voltage in a capacitor.
Step 1: Understand the initial conditions
Let the initial charge stored in the capacitor when connected to the battery of voltage V be Q. The relationship between charge Q, capacitance C, and voltage V is given by:
Q=C⋅V
Step 2: Determine the new conditions after reducing the voltage
When the potential difference is reduced by 100 V, the new voltage across the capacitor becomes V−100 volts. The charge stored in the capacitor at this new voltage is given by:
Q′=C⋅(V−100)
Step 3: Relate the charges before and after the voltage change
According to the problem, the charge stored after reducing the voltage becomes half of the initial charge:
Q′=Q2
Step 4: Substitute the expressions for charge
Substituting the expressions for Q and Q′ into the equation gives:
C⋅(V−100)=12⋅(C⋅V)
Step 5: Simplify the equation
We can cancel C from both sides (assuming C≠0):
V−100=12V
Step 6: Solve for V
To isolate V, we can multiply both sides by 2 to eliminate the fraction:
2(V−100)=V
Expanding this gives:
2V−200=V
Now, subtract V from both sides:
2V−V=200
This simplifies to:
V=200 volts
Final Answer
Thus, the value of V is:
200 volts
Let the initial charge stored in the capacitor when connected to the battery of voltage V be Q. The relationship between charge Q, capacitance C, and voltage V is given by:
Q=C⋅V
When the potential difference is reduced by 100 V, the new voltage across the capacitor becomes V−100 volts. The charge stored in the capacitor at this new voltage is given by:
Q′=C⋅(V−100)
According to the problem, the charge stored after reducing the voltage becomes half of the initial charge:
Q′=Q2
Substituting the expressions for Q and Q′ into the equation gives:
C⋅(V−100)=12⋅(C⋅V)
We can cancel C from both sides (assuming C≠0):
V−100=12V
To isolate V, we can multiply both sides by 2 to eliminate the fraction:
2(V−100)=V
Expanding this gives:
2V−200=V
Now, subtract V from both sides:
2V−V=200
This simplifies to:
V=200 volts
Thus, the value of V is:
200 volts
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 5
18 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Conceptual Questions
37 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 3
3 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
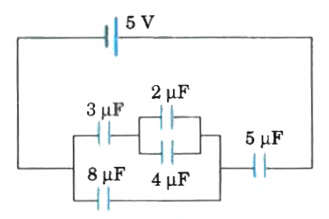
Five capacitors are connected across a battery of 5V as shown in figure (o). Calculate the potential difference across the plates of the 5μF capacitor.
View SolutionTwo, capacitors A and B are connected in series across a 100V supply and it is observed that the potential difference across them are 60V and 40V. A capacitor of 2p.F capacitance is now connected in parallel with A and the potential difference across B rises to 90V. Determine the capacitance of A and B
View Solution
Knowledge Check
Find the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
A0.02JB0.04JC0.01JD0.05JA capacitor of capacitance 500μF is charged at the rate of 100μC/s. The time in which the potential difference will become 20V, is :
A100sB50 sC20 sD10 s4μF capacitor is charged to 150 V and another capacitor of 6μF is charged to 200 V. Then they are connected across each other. Find the potential difference across them. Calculate the heat produced.
A0.005 JB0.500 JC0.003 JD1.003 J
Two capacitors of capacitance 6uF and 4uF are put in series across a 120V battery. What is the potential difference across the 4uF capacitor?
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts . The charge stored in it is 360μC . When potential across the capacitor is reduced by 120 V , the charge stored in it becomes 120 μC . Calculate :
The potential V and the unknown capacitance C .
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts . The charge stored in it is 360μC . When potential across the capacitor is reduced by 120 V , the charge stored in it becomes 120 μC . Calculate :
What will be the charge stored in the capacitor , if the voltage applied had increased by 120 V ?
View SolutionCalculate the capacity of unknown capacitance is connected across a battery of V volts. The charge stored in it is 360μC. When potential across the capacitor is reduced by 120V, the charge stored in it becomes 120μC.
Calculate (i) the potential V and unknown capacitance C. (ii) What will be the charge stored in the capacitor. If the voltage applied had increased by 120 V
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View Solution
