Find out the amount of the work done to separate the charges at infinite distance.
To find the amount of work done to separate two charges Q1 and Q2 from a distance r to an infinite distance, we can follow these steps:
Step 1: Understand the Concept of Electrostatic Potential Energy
The electrostatic potential energy U between two point charges Q1 and Q2 separated by a distance r is given by the formula:
U=14πϵ0Q1Q2r
where ϵ0 is the permittivity of free space.
Step 2: Determine Initial and Final Potential Energy
Initially, when the charges are at a distance r, the potential energy is:
Ui=14πϵ0Q1Q2r
When the charges are separated to an infinite distance, the potential energy becomes:
Uf=0
Step 3: Calculate the Work Done
The work done W to separate the charges is equal to the change in potential energy. Therefore, we can calculate it as:
W=Uf−Ui
Substituting the values we found:
W=0−14πϵ0Q1Q2r
This simplifies to:
W=−14πϵ0Q1Q2r
Step 4: Interpret the Result
The negative sign indicates that work is done against the electrostatic force between the two charges. To separate the charges, we need to do positive work, which means we need to provide energy equal to:
W=14πϵ0Q1Q2r
Final Answer
Thus, the amount of work done to separate the charges Q1 and Q2 to an infinite distance is:
W=14πϵ0Q1Q2r
---
The electrostatic potential energy U between two point charges Q1 and Q2 separated by a distance r is given by the formula:
U=14πϵ0Q1Q2r
where ϵ0 is the permittivity of free space.
Initially, when the charges are at a distance r, the potential energy is:
Ui=14πϵ0Q1Q2r
When the charges are separated to an infinite distance, the potential energy becomes:
Uf=0
The work done W to separate the charges is equal to the change in potential energy. Therefore, we can calculate it as:
W=Uf−Ui
Substituting the values we found:
W=0−14πϵ0Q1Q2r
This simplifies to:
W=−14πϵ0Q1Q2r
The negative sign indicates that work is done against the electrostatic force between the two charges. To separate the charges, we need to do positive work, which means we need to provide energy equal to:
W=14πϵ0Q1Q2r
Thus, the amount of work done to separate the charges Q1 and Q2 to an infinite distance is:
W=14πϵ0Q1Q2r
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Additional Questions)
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Fill in the Blanks)
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)
10 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionFind out the amount of the work done to separate the charges at infinite distance.
View Solution
Knowledge Check
A system consists of two charges 4μCand−3μC with no external field placed at (−5cm,0,0)and(0cm,0,0) respectively. The amount of work required to separated the two charges infinitely away from each other is
A−1.1JB2JC2.5JD3J
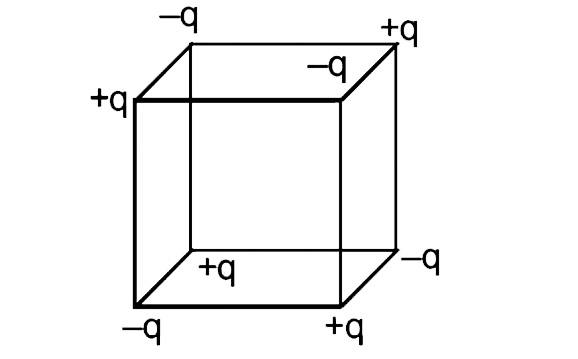
Charges +q and −q are located at the corners of a cube of side as show in the figure. Find the work done to separate the charges to infinite distance
View SolutionTwo point charges 9 μC and −2μC are placed at a separation of 20 cm from each other.
(i) Calculate the electric potential energy of this system of two charges.
(ii) What amount of work is required to separate the particles to infinite separation?
View SolutionThe ratio of the work done to the quantity of charge transferred .
View Solution(a) Use Gauss's theorem to find the electric field due to a uniformly charged infinitely
Iarge plane thin sheet with surface charge density.Σ
(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the
expression for the amount of work done in bringing a point charge q from infinity to a
point , distant r, in front of the charged plane sheet.
View SolutionThe ratio of the work done to the quantity of charge transferred .
View SolutionThree point charges +Q,+2Qand−3Q are placed at the vertices of an equilateral triangle ABC of side l. If these charges are displaced at the find points A1,B1andC1 respectively, find the amount of work done in shifting the charges to their new positions.
View Solution(a). Determine the potential energy of a system containing two charges 7μC and −2μC separated by a distance 18 cm. (b) How much work is needed to separate the two charges infinitely away from each other?
View Solution
