(a) Derive the expression for the capacitance of a parallel plate capacitor having plate area A and plate separation d.
(b) Two charged spherical conductors of radii and when connected by a conducting wire acquire charges respectively. Find the ratio of their surface charge densities in terms of their radii.
Step-by-Step Solution
1. Understanding the Setup:
- Consider two parallel plates separated by a distance d. The area of each plate is A.
- One plate is positively charged with charge +Q and the other is negatively charged with charge −Q.
2. Electric Field Between the Plates:
- The electric field E due to a single infinite plane sheet of charge is given by:
E=σ2ϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
- The surface charge density σ can be expressed as:
σ=QA
- Thus, the electric field due to the positive plate is:
E1=Q2Aϵ0
- The electric field due to the negative plate is directed towards it, hence:
E2=−Q2Aϵ0
3. Net Electric Field:
- The net electric field E between the plates is:
E=E1+E2=Q2Aϵ0−Q2Aϵ0=QAϵ0
4. Potential Difference:
- The potential difference V between the plates is given by:
V=E⋅d=(QAϵ0)d
5. Capacitance Definition:
- The capacitance C is defined as the charge per unit potential difference:
C=QV
6. Substituting for V:
- Substituting the expression for V:
C=Q(QAϵ0)d=Aϵ0d
7. Final Expression:
- Thus, the capacitance of a parallel plate capacitor is:
C=ϵ0Ad
Part (b): Ratio of Surface Charge Densities of Two Spherical Conductors
1. Understanding the Setup:
- Consider two spherical conductors with radii R1 and R2 that are connected by a conducting wire. They acquire charges Q1 and Q2 respectively.
2. Potential of Spherical Conductors:
- The potential V of a charged sphere is given by:
V=kQR
where k is Coulomb's constant.
3. Equal Potentials:
- Since the spheres are connected by a wire, their potentials must be equal:
V1=V2⟹kQ1R1=kQ2R2
- Simplifying gives:
Q1Q2=R1R2
4. Surface Charge Density:
- The surface charge density σ is given by:
σ=QA
where A is the surface area of the sphere, A=4πR2.
- Therefore, the surface charge densities are:
σ1=Q14πR21,σ2=Q24πR22
5. Finding the Ratio:
- The ratio of surface charge densities is:
σ1σ2=Q1/(4πR21)Q2/(4πR22)=Q1Q2⋅R22R21
- Substituting Q1Q2=R1R2:
σ1σ2=R1R2⋅R22R21=R2R1
6. Final Expression:
- Thus, the ratio of the surface charge densities is:
σ1σ2=R2R1
- Consider two parallel plates separated by a distance d. The area of each plate is A.
- One plate is positively charged with charge +Q and the other is negatively charged with charge −Q.
- The electric field E due to a single infinite plane sheet of charge is given by:
E=σ2ϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
- The surface charge density σ can be expressed as:
σ=QA
- Thus, the electric field due to the positive plate is:
E1=Q2Aϵ0
- The electric field due to the negative plate is directed towards it, hence:
E2=−Q2Aϵ0
- The net electric field E between the plates is:
E=E1+E2=Q2Aϵ0−Q2Aϵ0=QAϵ0
- The potential difference V between the plates is given by:
V=E⋅d=(QAϵ0)d
- The capacitance C is defined as the charge per unit potential difference:
C=QV
- Substituting the expression for V:
C=Q(QAϵ0)d=Aϵ0d
- Thus, the capacitance of a parallel plate capacitor is:
C=ϵ0Ad
- Consider two spherical conductors with radii R1 and R2 that are connected by a conducting wire. They acquire charges Q1 and Q2 respectively.
- The potential V of a charged sphere is given by:
V=kQR
where k is Coulomb's constant.
- Since the spheres are connected by a wire, their potentials must be equal:
V1=V2⟹kQ1R1=kQ2R2
- Simplifying gives:
Q1Q2=R1R2
- The surface charge density σ is given by:
σ=QA
where A is the surface area of the sphere, A=4πR2.
- Therefore, the surface charge densities are:
σ1=Q14πR21,σ2=Q24πR22
- The ratio of surface charge densities is:
σ1σ2=Q1/(4πR21)Q2/(4πR22)=Q1Q2⋅R22R21
- Substituting Q1Q2=R1R2:
σ1σ2=R1R2⋅R22R21=R2R1
- Thus, the ratio of the surface charge densities is:
σ1σ2=R2R1
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Numerical Problems)
25 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (MULTIPLE CHOICE QUESTIONS based on a given passage/comprehension)
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Short Answer Questions)
38 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Two charged spherical conductors of radii R1andR2 when connected by a connecting wire acquire charges q1andq2 respectively. Find the ratio of their charge densities in terms of their radil ?
View SolutionTwo chareged sperical conductors of radill R1andR2 when connected by a connecting wire acquire charges q1andq2 respectively. Find the ratio of their charge densities in terms of their radil ?
View Solution
Knowledge Check
A positive charge q is given to each plate of a parallel plate air capacitor having plate area A and plate separation d, then
Asince both the plates are identially charged, therefore, capacitance become equal to zeroBenergy stored in the space between the capacitor plates is equal to q2ε0A2Cno charge appears on inner surface of the platesDpotential difference between the plates is equal to 2qdε0AIn a parallel-plate capacitor of plate area A, plate separation d and charge Q the force of attraction between the plates is F.
AF∝Q2BF∝1ACF∝dDF∝1dTwo metallic s pheres of radii R1 and R2 are connected b y a thin wire. If +q1~and+q_(2) are the charges on the two s pheres then
Aq1/q2 = R1^2/ R2^2Bq1/q2 = R1/ R2Cq1/q2 = R1^3/ R2^3Dq1/q2 =( R1^2 -R2^2/ R1^2+ R2^2)
Two spherical conductors of radii R, and R2 (R2 > Ri) are charged. If they are connected by a conducting wire, find out the ratio of the surface charge densities on them.
View SolutionTwo charged spherical conductors of radius R1 and R2 are connected by a wire. Then the ratio of surface charge densities of the spheres σ1σ2 is
View SolutionA parallel plate capacitor having plate area A and separation between the plates d is charged to potential V.The energy stored in capacitor is ....???
View SolutionA parallel plate capacitor having a plate separation of 2mm is charged by connecting it to a 300V supply. The energy density is
View SolutionConsider a parallel plate capaciter having plates of unequal area. When a battery supplies +Q1 and −Q2 charges to two plates.
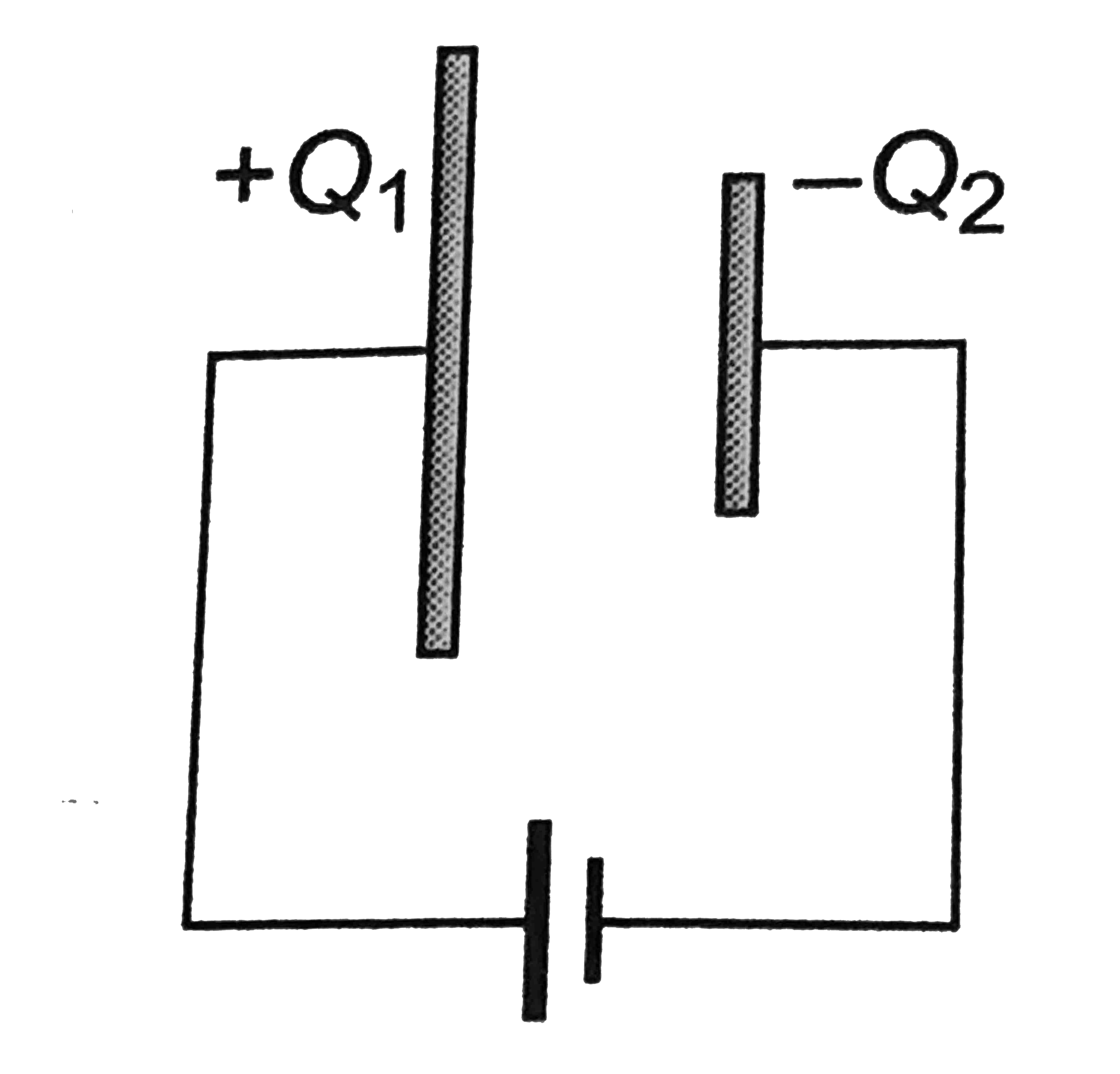
View Solution
