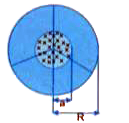
A line charge $l s m b d a$ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (refer to the figure given). A uniform magnetic field extends over a circular region within the rim. It is given by
$\to B = [- B_{0} 0 ˆ k (r \leq a, a < R) (otherwise)$
What is the angular velocity of the wheel after the field is suddenly switched off?

Text Solution

Verified by Experts

Area of wheel under the influence of magnetic field is
$A = π a^{2}$
The magnetic flux linked with area A is
$ϕ = π a^{2} B$
The induced emf in the loop is
$ε = - \frac{d ϕ}{d t} = - \frac{d}{d t} (B A) = - A \frac{d B}{d t} = - π a^{2} \frac{d B}{d t}$ ...(i)
The change in magnetic field B gives rise to the electric field E.
Work done in moving a charge q once around the loop of radius R is
$W = Electric force \times Distance = q E \times 2 π R$
$\Rightarrow \frac{W}{q} = 2 π R E$
Also, $ε = \frac{W}{q}$ (By definition of electric potential)
$\Rightarrow ε = 2 π R E$ ...(ii)
From (i) and (ii), we have
$- π a^{2} \frac{d B}{d t} = 2 π R E$
$\Rightarrow a^{2} d B = - 2 R E d t$ ...(iii)
Thus magnitude of average electric field developed can be written as follows:
$E = \frac{a^{2}}{2 R} \frac{Δ B}{Δ t}$
This electric field is along closed circular lines and the ring is also charged so it will apply tangential force on the ring to apply torque. Impulse of this torque will provide angular speed to ring.
$We know that, angular impulse = τ Δ t = q E R Δ t$ (in this case)
Also, if mass = M, then
Angular impulse = Change in angular momentum
$q E R Δ t = M R^{2} ω$ ( $ω$ is the angular velocity)
$q \frac{a^{2}}{2 R} \frac{Δ B}{Δ t} R Δ t = M R^{2} ω$
$ω = q \frac{a^{2}}{2} \frac{Δ B}{M R^{2}}$
Here, $Δ B = B_{0}$
$λ = \frac{q}{2 π R}$
$\Rightarrow ω = \frac{λ π a^{2} B_{0}}{M R}$
The distance of $ω$ will be along negative Z-axis.

Updated on:21/07/2023