Electric current in a circuit is given as a function of time as below .
I=I0(3t2τ)
Calculate the rms value of current for the time period t=0 to 2τ .
To find the RMS (Root Mean Square) value of the current given by the function I=I03t2τ over the time period from t=0 to t=2τ, we will follow these steps:
Step 1: Square the Current Function
First, we need to square the current function:
I2=(I03t2τ)2=I209t24τ2
Step 2: Set Up the Integral for the Mean
Next, we will calculate the mean of I2 over the interval from 0 to 2τ. The mean value of I2 is given by:
⟨I2⟩=1T∫T0I2dt
where T=2τ.
Step 3: Substitute and Integrate
Substituting I2 into the integral:
⟨I2⟩=12τ∫2τ0I209t24τ2dt
This simplifies to:
⟨I2⟩=I20⋅98τ3∫2τ0t2dt
Step 4: Calculate the Integral
Now, we need to calculate the integral ∫2τ0t2dt:
∫2τ0t2dt=(t33)2τ0=(2τ)33=8τ33
Step 5: Substitute Back into the Mean
Substituting this result back into the mean calculation:
⟨I2⟩=I20⋅98τ3⋅8τ33=9I203=3I20
Step 6: Calculate the RMS Value
Finally, the RMS value is the square root of the mean of I2:
Irms=√⟨I2⟩=√3I20=I0√3
Final Answer
Thus, the RMS value of the current is:
Irms=I0√3
---
First, we need to square the current function:
I2=(I03t2τ)2=I209t24τ2
Next, we will calculate the mean of I2 over the interval from 0 to 2τ. The mean value of I2 is given by:
⟨I2⟩=1T∫T0I2dt
where T=2τ.
Substituting I2 into the integral:
⟨I2⟩=12τ∫2τ0I209t24τ2dt
This simplifies to:
⟨I2⟩=I20⋅98τ3∫2τ0t2dt
Now, we need to calculate the integral ∫2τ0t2dt:
∫2τ0t2dt=(t33)2τ0=(2τ)33=8τ33
Substituting this result back into the mean calculation:
⟨I2⟩=I20⋅98τ3⋅8τ33=9I203=3I20
Finally, the RMS value is the square root of the mean of I2:
Irms=√⟨I2⟩=√3I20=I0√3
Thus, the RMS value of the current is:
Irms=I0√3
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - PRACTICE PROBLEMS67videos
ALTERNATING CURRENT
- BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - CONCEPTUAL QUESTIONS25videos
ALTERNATING CURRENT
- BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test16videos
ATOMS
Similar Questions
The current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe electric current flowing in a circuit is given by i=((2t)/(3 tau)) A for some time.The rms value of current for the period t=0 to t=tau is
View Solution
Knowledge Check
- Question 1 - Select One
The average value of current for the current shown for time period 0 to T2 s
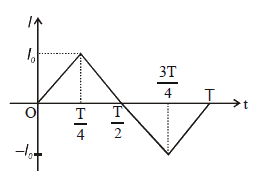 Al0√2Bl02Cl0√3Dl02√3
Al0√2Bl02Cl0√3Dl02√3 - Question 2 - Select One
The electric current in AC circuit is given by the relation i =3sinωt+4cosωt. The rms value of the current in the circuit in ampere is
A5√2B5√2C√25D1√2 - Question 3 - Select One
If i=t2,0<t<T then r.m.s. value of current is
AT2√2BT22CT2√5DNone of these
The electric current flowing in a circuit is given by i=(2t)/(3 tau) A for some time.The rms value of current for the period t=" to t=tau is O (2)/(sqrt(3))" A
View SolutionThe current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe electric current in a circuit is given by I=2i0/τ for some time. What is the rms current for the period t=0 to t=τ ?
View SolutionThe electric current in a circuit is given by I=2i0/τ for some time. What is the rms current for the period t=0 to t=τ ?
View SolutionThe electric current in a circuit is given by I = 3 sin ωt+4cosωt. The rms current is
View Solution

