A capacitor of capacitance 2 μF is connected to an osillator giving an output voltage e = 20 sin ω t volt . If ω=10π rad/ s write an equation for instantaneous current through the circuit .
To find the instantaneous current through a capacitor connected to an AC source, we can follow these steps:
Step 1: Identify the given values
- Capacitance C=2μF=2×10−6F
- Voltage e(t)=20sin(ωt)
- Angular frequency ω=10πrad/s
Step 2: Write the expression for the capacitive reactance Xc
The capacitive reactance Xc is given by the formula:
Xc=1ωC
Substituting the values:
Xc=110π×2×10−6=120π×10−6=10620πΩ
Calculating Xc:
Xc≈10662.83≈15915.5Ω
Step 3: Calculate the maximum current I0
The maximum current I0 can be calculated using the formula:
I0=E0Xc
Where E0=20V:
I0=2015915.5≈0.001255A=1.255mA
Step 4: Write the equation for instantaneous current
In a capacitive circuit, the current leads the voltage by π2 radians. Therefore, the instantaneous current i(t) can be expressed as:
i(t)=I0sin(ωt+π2)
Substituting the values of I0 and ω:
i(t)=1.255sin(10πt+π2)mA
Final Answer
The equation for the instantaneous current through the circuit is:
i(t)=1.255sin(10πt+π2)mA
---
- Capacitance C=2μF=2×10−6F
- Voltage e(t)=20sin(ωt)
- Angular frequency ω=10πrad/s
The capacitive reactance Xc is given by the formula:
Xc=1ωC
Substituting the values:
Xc=110π×2×10−6=120π×10−6=10620πΩ
Calculating Xc:
Xc≈10662.83≈15915.5Ω
The maximum current I0 can be calculated using the formula:
I0=E0Xc
Where E0=20V:
I0=2015915.5≈0.001255A=1.255mA
In a capacitive circuit, the current leads the voltage by π2 radians. Therefore, the instantaneous current i(t) can be expressed as:
i(t)=I0sin(ωt+π2)
Substituting the values of I0 and ω:
i(t)=1.255sin(10πt+π2)mA
The equation for the instantaneous current through the circuit is:
i(t)=1.255sin(10πt+π2)mA
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - PRACTICE PROBLEMS67videos
ALTERNATING CURRENT
- BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - CONCEPTUAL QUESTIONS25videos
ALTERNATING CURRENT
- BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test16videos
ATOMS
Similar Questions
A capacitor of capacitance 10μF is connected to an oscillator giving an output voltage ε=(10V)sinωt. Find the peak currents in the circuit for ω=10s−1,100s−1,500s−1,1000s−1.
View SolutionA capacitor of capacitive reactance 5ω is connected with A.C. source having voltage V=3sin(ωt+π/6). Find rms and Peak voltage rms and peak current and instantaneous current
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A capacitor of capacity C is connected in A.C circuit. If the applied emf is V=V0sinωt, then the current is
AI=V0LωsinωtBI=V0ωCsin(ωt+π2)CI=V0CωsinωtDt=V0Cωsin(ωt+π2) - Question 2 - Select One
A capacitor of capacitance 12(μ)Fis connected to a battery of emf 6.00V and internal resistance 1.00(Ω)through resistanceless leads. 12.0(μ)s after the connections are made, what will be (a) the current in the circuit, (b)the power delivered by the battery ,(c)the power dissipated in heat and (d)the rate at which the energy stored in the capacitor is increasing.
A4.42AB6AC2.21AD0A - Question 3 - Select One
A capacitor of capacitance 20μF is connected in series with 25Ω resistance to 240 V, 50 Hz AC. The maximum current in the circuit is
A14.9 AB1.49 AC2.49 AD2.89 A
An alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
View SolutionIn the circuit below, the AC source the voltage V=20cos(ωt) volts with ω=2000rad/sec. The amplitude of the current will be nearest to
 View Solution
View SolutionAn alternative voltage V=10sinωt (in volts) is applied across a parallel arrangement as shown current (in A) through the source is best described by
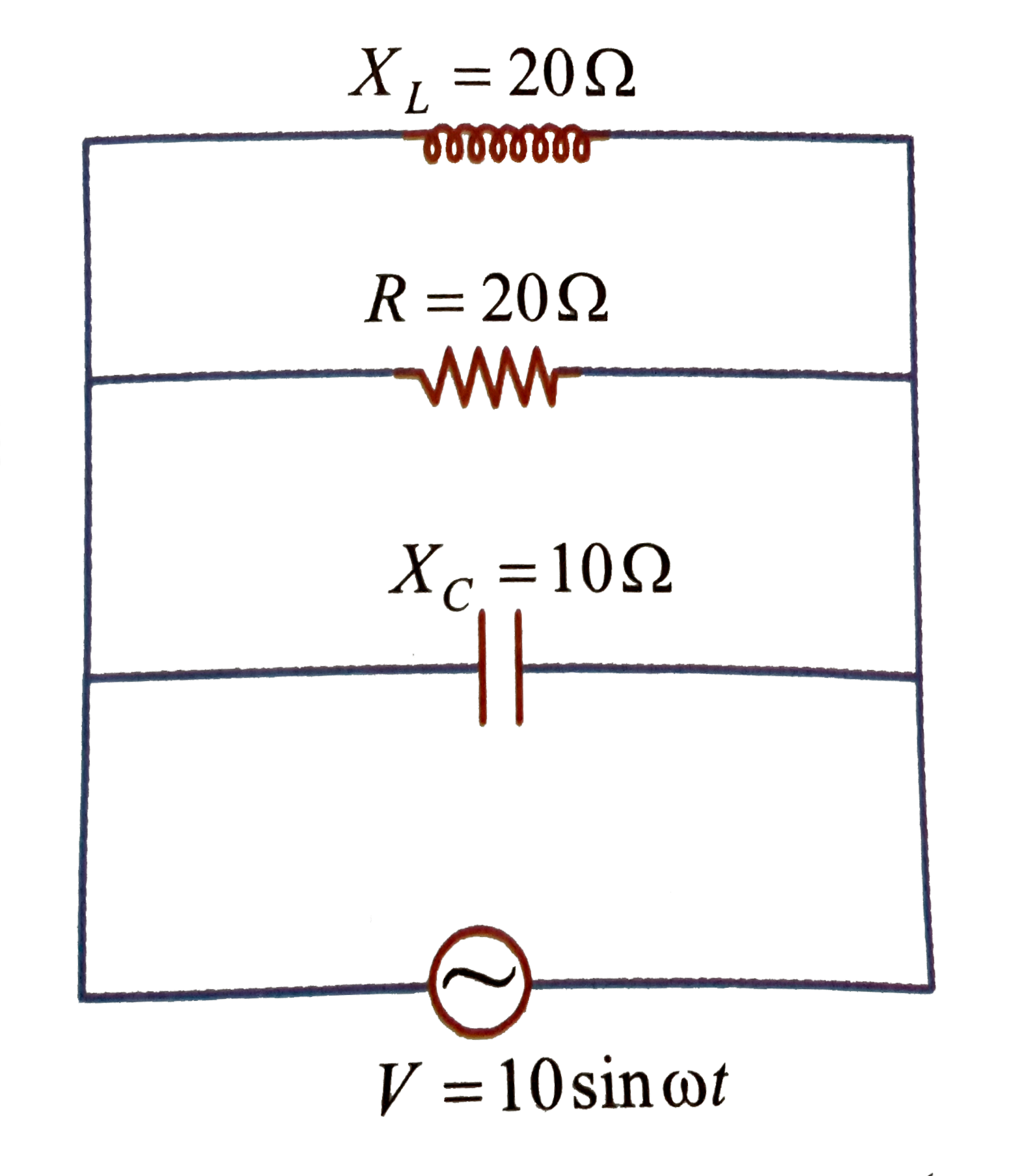 View Solution
View SolutionAn uncharged capacitor of capacitance 8.0μF is connected to a battery of emf 6.0 V through a resistance of 24Ω, then
(ii) The current in the circuit at one time constant after the connections are made is :View SolutionIn an ac circuit , an alternating voltage e=200√2sin100t volts is connected to a capacitor of capacitance 1μF. The rms value of the current in the circuit is :
View Solution

