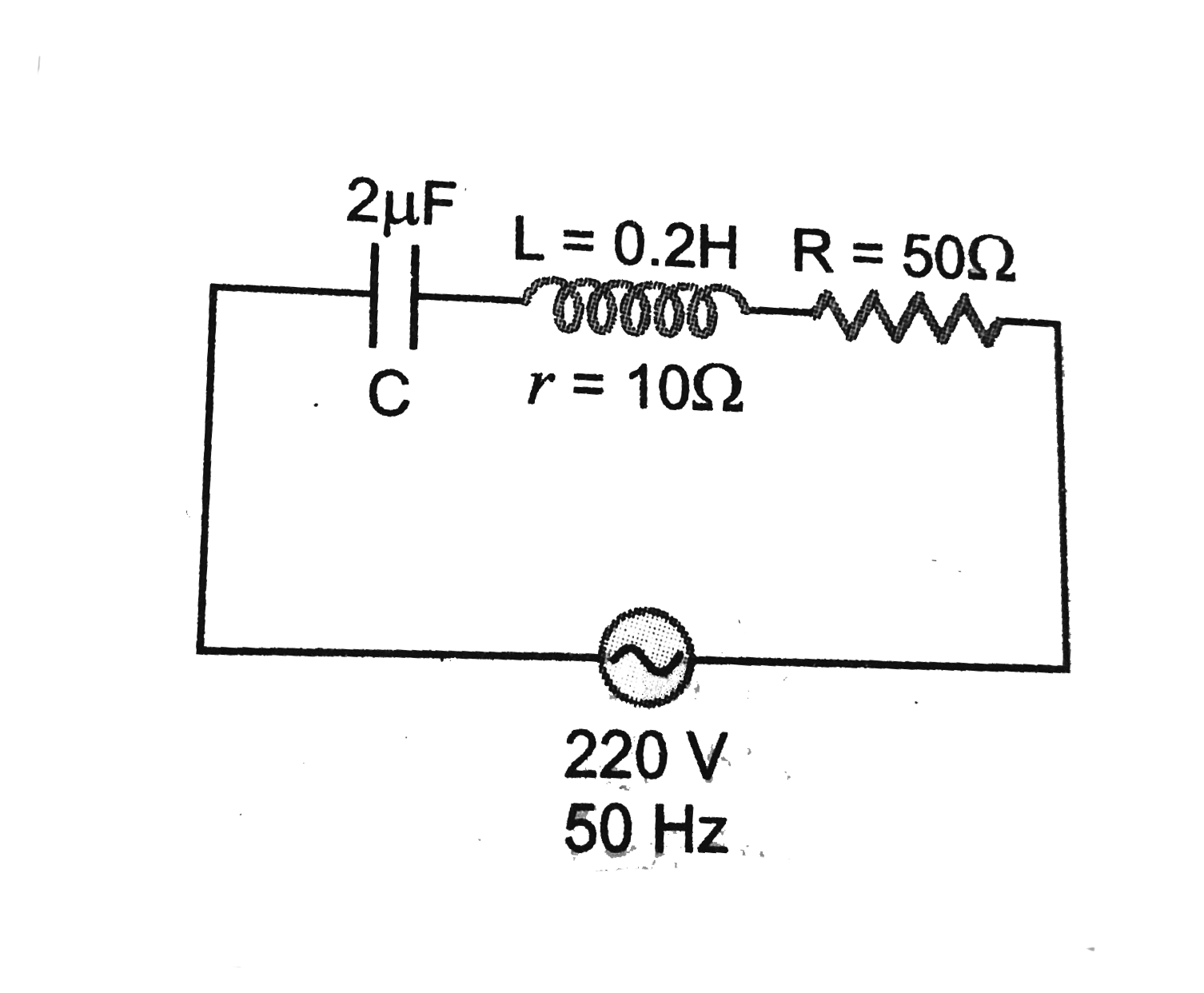
An AC circuit is shown below consisting of series combination of an inductor and a resistor .

(i) Calculate the rms value of applied voltage.
(ii) Also calculate the total impedance of the circuit if the rms current in the circuit be 2 A.
(iii) What will be the potential difference in the circuit if the direct current is passed?
(i) In series L -R circuit VR is in phase with current I and VL is π/2 rad ahead of current I. So the phase difference between VR and VL is π2=(90∘) .

Vrms=√V2R+V21=√1102+1202=162 V
(ii) Impedance of the circuit is
Z=VrmsIrms
Given Irms=2A
∴Z=162281Ω
(iii) In case of direct current through the circuit the reactance (ωL) of the circuit becomes zero . ∴ The potential difference in teh circuit =VR=150V
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - PRACTICE PROBLEMS
67 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - CONCEPTUAL QUESTIONS
25 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
Knowledge Check
In the circuit shown, rms circuit is 11 A . The potential difference across the inductor is
 A220 VB0 VC300 VD200 V
A220 VB0 VC300 VD200 VThe rms value of current in an ac circuit is 25 A, then peak current is
A35.36mAB35.36AC3.536AD49.38AThe rms value of current in an ac circuit is 25 A, then peak current is
A35.36mAB35.36AC3.536AD49.38A
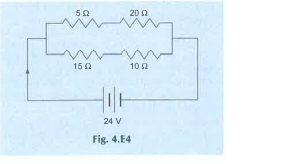
In the circuit shown in Fig. calculate
(i) current in the circuit
(ii) Potential difference across each element.
View SolutionAn a.c. voltage of 100 V, 50 Hz is connected across a 20 ohm resistor and 2 mH inductor in series. Calculate ltbr gt (i) impedance of the circuit,
(ii) rms current in the circuit.
View SolutionFor the given circuit diagram calculate:
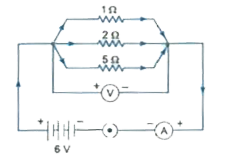
(i) the current through each resistor.
(ii) the total current in the circuit.
(iii) the total effective resistance of the circuit
View SolutionAn a.c. voltage of 100 V, 50 Hz is connected across a 20 Ω resistance and a 2 mH inductor in series. Calculate (1) impedance of the circuit, (ii) rms current in the circuit.
View SolutionDerive an expression for the impedance of an a.c. circuit consisting of an inductor and a resistor.
View Solution