What is the average value of alternate voltage and current in a complete cycle ?
To find the average value of alternating voltage and current over a complete cycle, we can follow these steps:
1. Understand the Functions:
The voltage and current in an AC circuit can be represented as sinusoidal functions. For voltage, we have:
V(t)=V0sin(ωt+ϕ)
and for current:
I(t)=I0sin(ωt+ϕ′)
where V0 and I0 are the peak values, ω is the angular frequency, and ϕ and ϕ′ are the phase angles.
2. Average Value Definition:
The average value of a function f(t) over a period T is given by:
Average=1T∫T0f(t)dt
For our case, we will apply this to both voltage and current.
3. Integral Calculation:
For a complete cycle (from 0 to T):
- The average voltage Vavg is:
Vavg=1T∫T0V(t)dt=1T∫T0V0sin(ωt+ϕ)dt
- The average current Iavg is:
Iavg=1T∫T0I(t)dt=1T∫T0I0sin(ωt+ϕ′)dt
4. Evaluate the Integrals:
The integral of a sine function over a complete cycle (from 0 to T) is zero:
∫T0sin(ωt+ϕ)dt=0
Therefore:
Vavg=1T⋅V0⋅0=0
and similarly,
Iavg=1T⋅I0⋅0=0
5. Conclusion:
The average value of both the alternating voltage and current over a complete cycle is:
Vavg=0andIavg=0
The voltage and current in an AC circuit can be represented as sinusoidal functions. For voltage, we have:
V(t)=V0sin(ωt+ϕ)
and for current:
I(t)=I0sin(ωt+ϕ′)
where V0 and I0 are the peak values, ω is the angular frequency, and ϕ and ϕ′ are the phase angles.
The average value of a function f(t) over a period T is given by:
Average=1T∫T0f(t)dt
For our case, we will apply this to both voltage and current.
For a complete cycle (from 0 to T):
- The average voltage Vavg is:
Vavg=1T∫T0V(t)dt=1T∫T0V0sin(ωt+ϕ)dt
- The average current Iavg is:
Iavg=1T∫T0I(t)dt=1T∫T0I0sin(ωt+ϕ′)dt
The integral of a sine function over a complete cycle (from 0 to T) is zero:
∫T0sin(ωt+ϕ)dt=0
Therefore:
Vavg=1T⋅V0⋅0=0
and similarly,
Iavg=1T⋅I0⋅0=0
The average value of both the alternating voltage and current over a complete cycle is:
Vavg=0andIavg=0
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Revision Exercises ( Additional Questions )
10 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Revision Exercises (Fill in the Blanks )
10 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
7 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
Knowledge Check
The average value of alternating current over a complete cycle is
AzeroB1 rmsCI√2D2IThe average value of alternating current for half cycle in terms of I0 is
A2I0πBI0πCi0√2D0The rms and the average value of the voltage wave shown in figure are
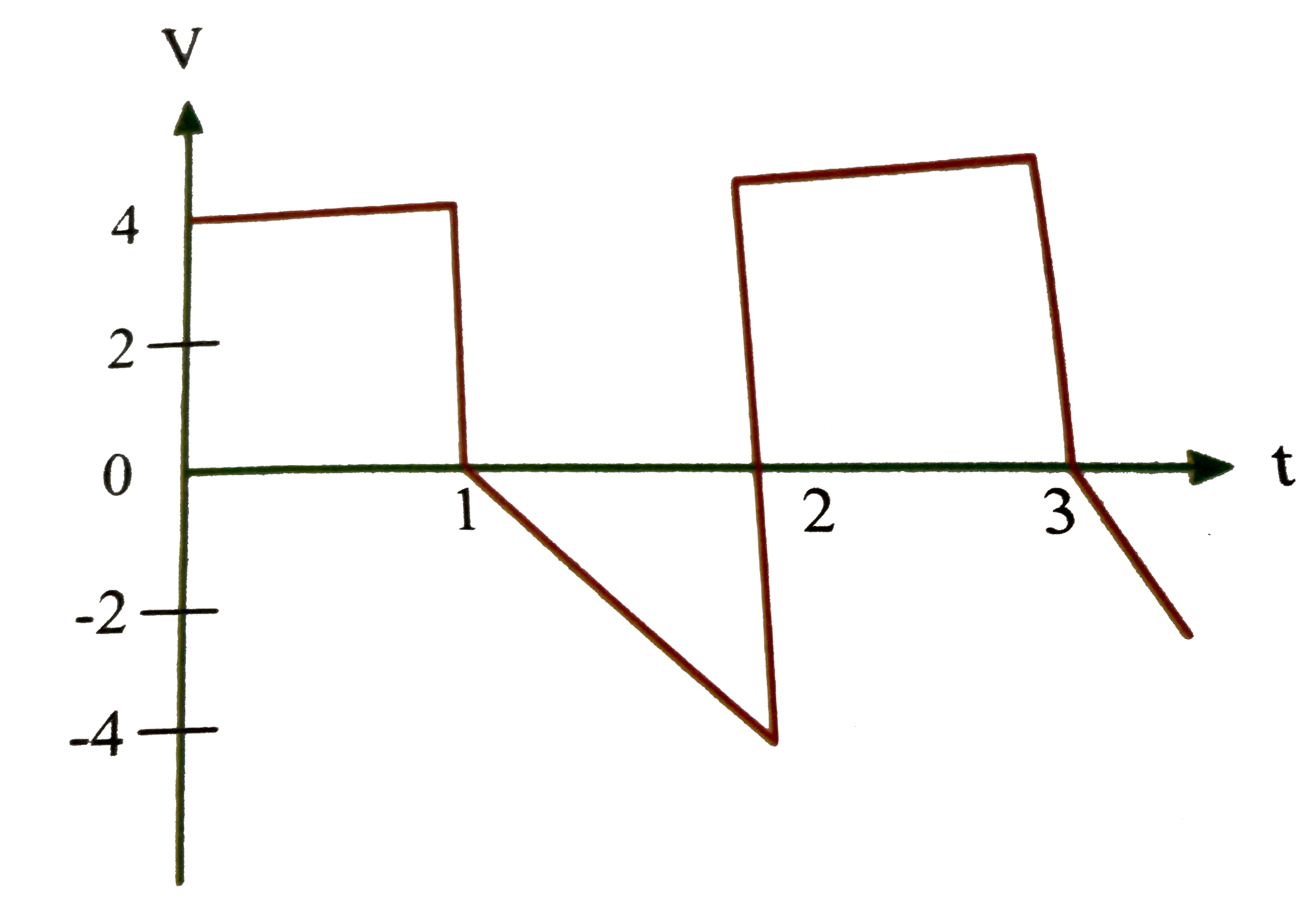 A√323V,1VB√113V,1VC√113V,3VD√323V,3V
A√323V,1VB√113V,1VC√113V,3VD√323V,3V
What is the average value of a.c. over a full cycle ?
View SolutionWhen an a.c. source is connected across an ideal inductor,show on a graph the nature of variation of the voltage and the current over one complete cycle.
View SolutionDefine average value of alternating current . Derive an expression for it .
View SolutionThe average value of an alternating voltage V=V0sinωt over a full cycle is
View SolutionIn an a.c circuit, value of voltage and current change every instant. Therefore, power of an a.c. circuit at any instant is the product of instantaneous voltages (E) and instantaneous current (I). The average power supplied to a pure resistance R over a complete cycle of a.c is P=Eυ.Iυ. When circuit is inductive, average power/cycle =EυIυcosϕ, where ϕ is the phase angle between alternating voltage an altenating current in the circuit.
In an a.c. circuit, 800mH inductor and a 60μF capacitor are connected in series with 15ohm resistance. The a.c. supply to the circuit is 230V,50Hz
The average power transferred per cycle ot capacitor is
View Solution
