There is one long straight conductor carrying current which is kept along the dimaeter of a circular loop without touching it.
emf induced in the loop is zero if AC current is flowing through the straight conductor
emf induced in the loop is zero if current in the straight conductor increases.
emf induced in the loop is zero if current in the straight conductor decreases.
emf induced in the loop is zero constant current flows through the straight conductor .
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the situation of a long straight conductor carrying current placed along the diameter of a circular loop. We will examine the implications of this configuration on the induced electromotive force (EMF) in the loop.
1. Understanding the Configuration:
- We have a circular loop and a straight conductor placed along its diameter.
- The conductor carries a current (let's denote it as I).
2. Magnetic Field Due to the Straight Conductor:
- According to Ampère's Law, a long straight conductor carrying current produces a magnetic field around it.
- The direction of the magnetic field can be determined using the right-hand rule. If the current flows in a certain direction, the magnetic field will circulate around the conductor.
3. Analyzing the Magnetic Field in the Loop:
- The magnetic field produced by the straight conductor will be different in the upper and lower halves of the circular loop.
- For the upper half of the loop, if the current is flowing from left to right, the magnetic field will be directed out of the plane (towards us).
- For the lower half of the loop, the magnetic field will be directed into the plane (away from us).
4. Calculating the Magnetic Flux:
- The magnetic flux (Φ) through the loop is given by the product of the magnetic field (B) and the area (A) it penetrates: Φ=B⋅A.
- Since the area of the upper half and lower half of the loop is equal, we can denote the magnetic flux in the upper half as Φ=φ and in the lower half as Φ=−φ.
- Therefore, the net magnetic flux through the loop is:
Φnet=φ+(−φ)=0
5. Induced EMF Calculation:
- According to Faraday's law of electromagnetic induction, the induced EMF (ε) in a loop is given by the rate of change of magnetic flux through the loop:
ε=−dΦdt
- Since the net magnetic flux Φnet=0, the rate of change of flux dΦdt will also be zero:
ε=−d(0)dt=0
6. Conclusion:
- Regardless of whether the current in the conductor is constant, increasing, or decreasing, the induced EMF in the loop remains zero.
Final Answer:
The induced EMF in the loop is zero.
- We have a circular loop and a straight conductor placed along its diameter.
- The conductor carries a current (let's denote it as I).
- According to Ampère's Law, a long straight conductor carrying current produces a magnetic field around it.
- The direction of the magnetic field can be determined using the right-hand rule. If the current flows in a certain direction, the magnetic field will circulate around the conductor.
- The magnetic field produced by the straight conductor will be different in the upper and lower halves of the circular loop.
- For the upper half of the loop, if the current is flowing from left to right, the magnetic field will be directed out of the plane (towards us).
- For the lower half of the loop, the magnetic field will be directed into the plane (away from us).
- The magnetic flux (Φ) through the loop is given by the product of the magnetic field (B) and the area (A) it penetrates: Φ=B⋅A.
- Since the area of the upper half and lower half of the loop is equal, we can denote the magnetic flux in the upper half as Φ=φ and in the lower half as Φ=−φ.
- Therefore, the net magnetic flux through the loop is:
Φnet=φ+(−φ)=0
- According to Faraday's law of electromagnetic induction, the induced EMF (ε) in a loop is given by the rate of change of magnetic flux through the loop:
ε=−dΦdt
- Since the net magnetic flux Φnet=0, the rate of change of flux dΦdt will also be zero:
ε=−d(0)dt=0
- Regardless of whether the current in the conductor is constant, increasing, or decreasing, the induced EMF in the loop remains zero.
The induced EMF in the loop is zero.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE D. MULTIPLE CHOICE QUESTIONS
13 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE ASSERTION REASON TYPE QUESTIONS
10 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE JEE (ADVANCED ) FOR IIT ENTRANCE
4 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
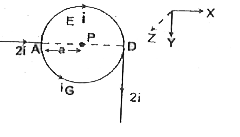
In the shown figure a current 2i is flowing in a straight conductor and entering along the diameter of the circular loop of similar conductor through the point A. The current is leaving the loop along another similar semi-infinite conductor parallel to the plane of the loop through the point D. what is the magnetic field at the centre of the loop P ?
View SolutionA current flows clockwise in a flat square loop. In the plane of the loop there lies an infInitely long straight conductor carrying a current whose direction is designated by the arrow in the figure. How will the loop move in the magnetic field created by the current flowing in the straight conductor and how wi ll the shape of the loop change as a result of the action of this field?
View Solution
Knowledge Check
A current-carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it. The correct statement(s) is (are)
AThe emf induced in the loop is zero if the current is constant.BThe emf induced in the loop is finite if the current is constant.CThe emf induced in the loop is zero if the current decreases at a steady rate.DThe emf induction in the loop is finite if the current decreases at a steady rate.A current-carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it. The correct statement(s) is (are)
AThe emf induced in the loop is zero if the current is constant.BThe emf induced in the loop is finite if the current is constant.CThe emf induced in the loop is zero if the current is decreases at a steady rate.DThe emf induced in the loop is infinite if the current is decreases at a steady rate.A long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop
 Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)
Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)
An infinitely long, straight wire carrying current I1 passes through the center of circular loop of wire carrying current I2. The infinite wire is perpendicular to the plane ofthe loop. Which of the following statements is/are INCORRECT regarding the magnetic force on the loop due to the infinite wire:
View SolutionA current- carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
View SolutionA long straight conductor carrying a current lies along the axis of a ring. The conductor will exert a force on the ring if the ring
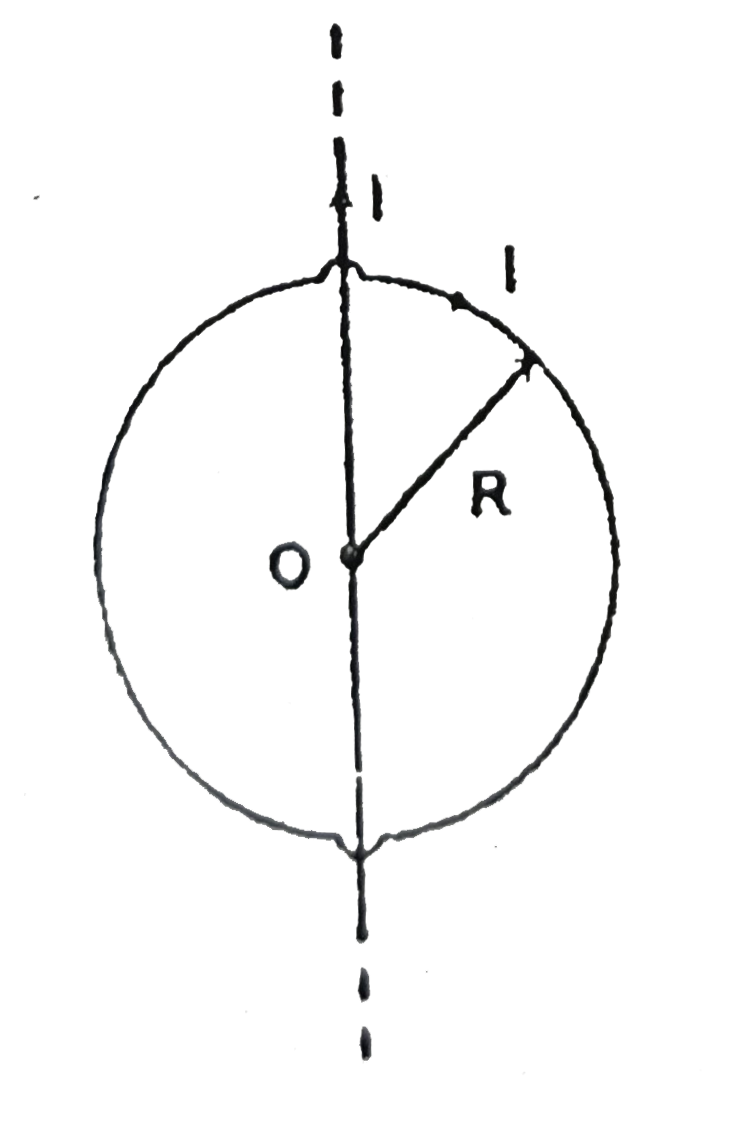
View SolutionA circular conducting loop of radius R carries a current I. Another straight infinite conductor carrying current I passes through the diameter of this loop as shown in the figure. The magnitude of force exerted by the straight conductor on the loop is
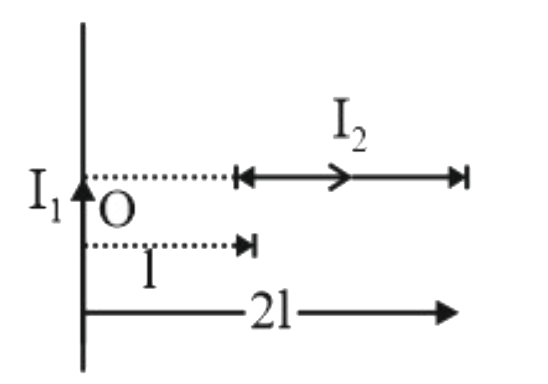
View SolutionA finite carrying - current wire is placed in a plane along with very long ,straight conductor carrying current as shown in the figure. The torque on the finite current wire about point O is
View Solution
