Assertion : in case of DC circuit , current through the branch of capacitor is zero .
Reason : Reactance of the capacitor is 1/ωC and ω for the DC source can be assumed to the zero, hence reactance of capacitor for DC circuit becomes infinite .
If both assertion and reason are correct and reason is a correct explanation of the assertion
If both assertion and reason are correct but reason is not the correct explanation of assertion
If assertion is correct but reason is incorrect
If assertion is inncorrect but reason is correct
The correct Answer is:A
To solve the question, we need to analyze the assertion and the reason provided.
Assertion: In case of a DC circuit, the current through the branch of a capacitor is zero.
Reason: The reactance of the capacitor is given by Xc=1ωC, and for a DC source, ω can be assumed to be zero. Hence, the reactance of the capacitor for a DC circuit becomes infinite.
1. Understanding DC Circuits:
- In a Direct Current (DC) circuit, the current flows steadily in one direction. The voltage is constant over time.
2. Capacitor Behavior in DC Circuits:
- A capacitor stores electrical energy when connected to a voltage source. Initially, when connected to a DC source, it allows current to flow until it is fully charged.
3. Reactance of a Capacitor:
- The reactance Xc of a capacitor is defined as:
Xc=1ωC
- Here, ω is the angular frequency of the AC source, and C is the capacitance.
4. Angular Frequency in DC Circuits:
- For a DC source, the frequency is zero (f=0), which means:
ω=2πf=0
5. Calculating Reactance for DC:
- Substituting ω=0 into the reactance formula:
Xc=10→∞
- This indicates that the reactance of the capacitor in a DC circuit is infinite.
6. Implication of Infinite Reactance:
- An infinite reactance means that the capacitor behaves like an open circuit. Hence, no current can flow through the capacitor branch in a DC circuit.
7. Conclusion:
- Therefore, the assertion that the current through the branch of a capacitor in a DC circuit is zero is correct.
- The reason provided is also correct as it explains why the current is zero due to the infinite reactance of the capacitor when connected to a DC source.
Final Statement:
Both the assertion and the reason are correct, and the reason provides a correct explanation for the assertion.
---
- In a Direct Current (DC) circuit, the current flows steadily in one direction. The voltage is constant over time.
- A capacitor stores electrical energy when connected to a voltage source. Initially, when connected to a DC source, it allows current to flow until it is fully charged.
- The reactance Xc of a capacitor is defined as:
Xc=1ωC
- Here, ω is the angular frequency of the AC source, and C is the capacitance.
- For a DC source, the frequency is zero (f=0), which means:
ω=2πf=0
- Substituting ω=0 into the reactance formula:
Xc=10→∞
- This indicates that the reactance of the capacitor in a DC circuit is infinite.
- An infinite reactance means that the capacitor behaves like an open circuit. Hence, no current can flow through the capacitor branch in a DC circuit.
- Therefore, the assertion that the current through the branch of a capacitor in a DC circuit is zero is correct.
- The reason provided is also correct as it explains why the current is zero due to the infinite reactance of the capacitor when connected to a DC source.
Both the assertion and the reason are correct, and the reason provides a correct explanation for the assertion.
Topper's Solved these Questions
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:COMPETITION FILE INTEGER TYPE QUESTIONS
Explore 11 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:COMPETITION FILE EXEMPLAR PROBLEMS (OBJECTIVE QUESTIONS ) (Multiple choice question (Type ) )
Explore 13 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:COMPETITION FILE D. MULTIPLE CHOICE QUESTIONS
Explore 13 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
Knowledge Check
The capacitive reactance of a capacitor is d.c. circuit in ohm is
AzeroBωCC1/ωCD∞The conduction current in ideal case through a circuit is zero when charge on capacitor is
AzeroBmaximumCany transient valueDdepends on capacitor usedAssertion: In the circuit shown in figure no charge will stored in the capacitor.
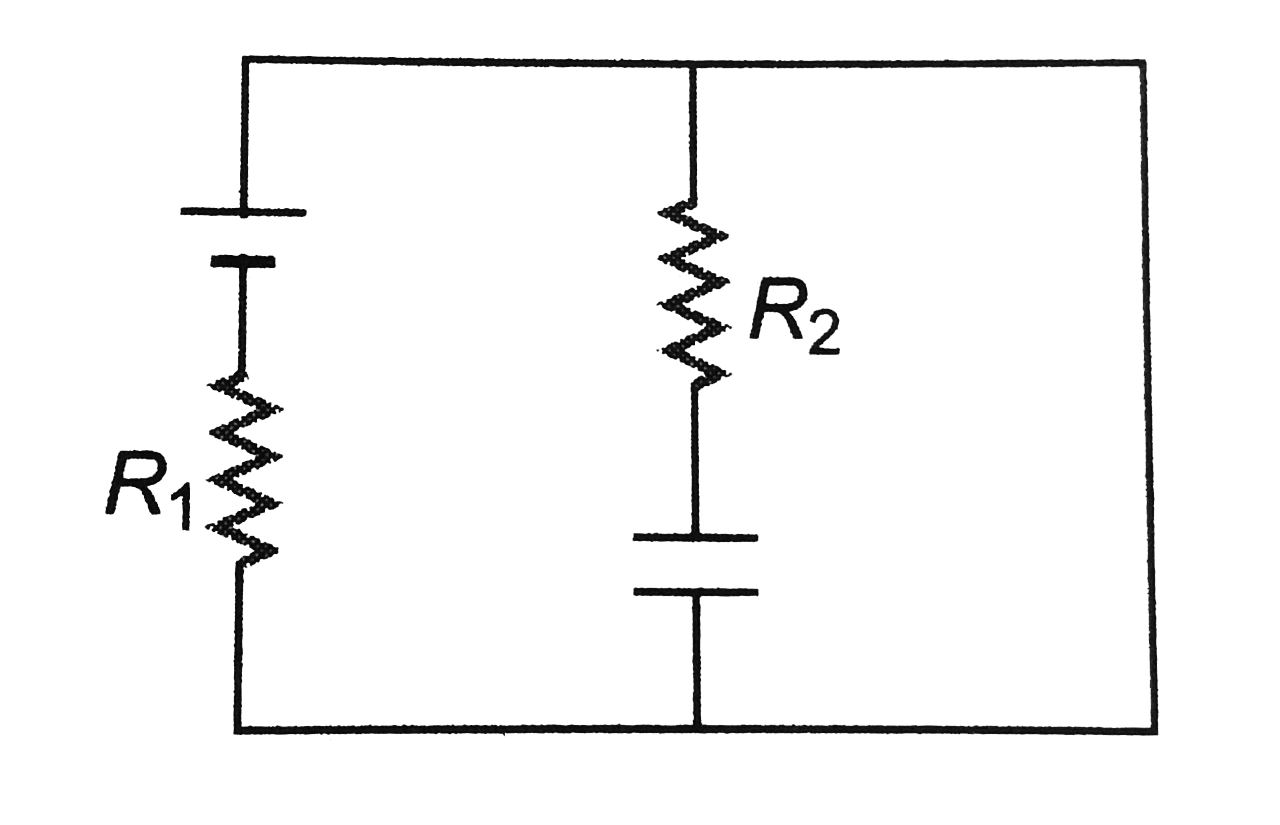
Reason: Current through R2 will be zero.AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.CIf Assertion is true, but the Reason is false.DIf Assertion is false but the Reason is true.
What is the value of capacitive reactance (XC) in DC circuits ?
View SolutionFind capacitive reactance of a capacitor connected to a dc source.
View SolutionConsider the following two statements A and B and identify the correct answer.
A) At resonance of L−C series circuit, the reactance of circuit is minimum.
B) The reactance of a capacitor is an A.C circuit is similar to the reactance of a capacitor in a D.C circuit
View SolutionThe reactance of a capacitor in an A.C. circuit is 10Ω. If the frequency of A.C. is doubled, its reactance will become
View SolutionWhen a capacitor is connected to a voltage source in a DC circuit, current will flow for the short time required to charge the capacitor.
As charge accumulates on the capacitor plates, the voltage across them increases,opposing the current.
A capacitor in a DC circuit will limit or oppose the current.
When the capacitor is fully charged , the current in the circuit falls to zero.
Which of the above statements are correct> Choose the correct option.
View Solution