A nucleus A, With a finite de-broglie wavelength λA, undergoes spontaneous fission into two nuclei B and C of equal mass. B flies in the same direction as that of A, While C flies in the opposite direction with a velocity equal to half of that of B . The de-Broglie wavelength λB and λB and C are respectively:
λA,2λA
2λA,λA
λA,λA2
λA2,λA
The correct Answer is:D
Let 2m be the mass of A and moving with velocity v0 There are two equal nuclei hence mass of each is m. Velocity of B is v then velocity of C will be v/2 in opposite directions as shown in diagram
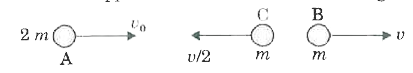
According to principal of conservation of linear momentum we can write the following .
2mv0=mv−mv/2⇒v=4v0
Linear momentum of particles are as follows.
PA=2mv0=PB=4mv0andPC=2mv0
De - Broglie wavelength λ=h/p
λA=h2mv0,λB=h4mv0=λA2,λC=h2mv0=λA
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( B - Multiple Choice Questions) (JEE (Advanced) for IIT Entrance))
15 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( C - Multiple Choice Questions) )
8 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( B - Multiple Choice Questions) (AIPMT/NEET & Other State Boards for Medical Entrance))
26 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Chapter Practice Test
15 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A particle A of mass m and initial velocity v collides with a particle of mass m/2 which is at rest. The collision is head on, and elastic. The ratio of the de-broglie wavelength λAandλB after the collision is
View SolutionTwo particles A and B of de-broglie wavelength λ1andλ2 combine to from a particle C. The process conserves momentum. Find the de-Broglie wavelength of the particle C. (The motion is one dimensional).
View Solution
Knowledge Check
A particle A of mass m and initial velocity v collides with a particle of mass m/2 which is at rest. The collision is head on, and elastic. The ratio of the de-broglie wavelength λAandλB after the collision is
AλAλB=23BλAλB=12CλAλB=13DλAλB=2A particle of mass 3 m at rest decay Into two particles of masses m and 2m having non-zero velocities. What is the ratio of the de-Broglie wavelengths of the particle (λ1/λ2).
A1:1B1:2C3:2D2:1A particle of mass M at rest decay's into two particle of masses m1 and m2 having non zero velocity. The ratio of the de Broglie wavelengths of the masses λ1/λ2 is
Am1/m2Bm2/m1C1.0D√m1/√m2
An electron, a doubly ionized helium ion (He++) and a proton are having the same kinetic energy . The relation between their respectively de-Broglie wavelengths λe,λHe++ and λp is :
View SolutionFind the ratio of de-Broglie wavelengths associated with two electrons A and B which are accelerated 8V and 64 Volts respectively.
View SolutionWhen photones of energy 4.0 eV fall on the surface of a metal A, the ejected photoelectrons have maximum kinetic energy TA ( in eV) and a de-Broglie wavelength λA. When the same photons fall on the surface of another metal B, the maximum kinetic energy of ejected photoelectrons is TB=TA−1.5eV. If the de-Broglie wavelength of these photoelectrons is λB=2λA, then the work function of metal B is
View SolutionThe de-Broglie wavelength (λB) associated with the electron orbiting in the second excited state of hydrogen atom is related to that in the ground state (λG) by :
View SolutionA particle A moving with a certain velocity has a de Broglie wavelength of 1 A. If particle B has mass 25% of that A and velocity 75% of that of A, the de Broglie wavelength of B will be approximately
View Solution
