In the given figure, quadrilateral ABCD is a quadrilateral in which AB = AD and BC = DC. Prove that (i) AC bisects ∠A and ∠B, (ii) AC.is the perpendicular bisector of BD.
1)∠ABCand∠ADC
AB=AD
BC=DC
AC=AC
∠ABC≅∠ADC(SSS)
∠BAE=∠DAE
∠BAE=∠DAE
AC is a bisector of ∠A
2)BE=BD
∠ABEand∠AED
BE=ED
AB=AD
AE=AE
∠ABE≅∠AED(SSS)
So, ∠AED=∠AEB
∠AEB+∠AED=1800
∠AEB=900.
Similar Questions
If ABCD is a quadrilateral such that AB = AD and CB = CD , then prove that AC is the perpendicular bisector of BD.
View SolutionIn the figure ABCD is a quadrilateral in which AB=AD And BC=DC Prove that AC bisects A and C at each angle.
View SolutionIn the figure ABCD is a quadrilateral in which AB=AD And BC=DC Prove that BE=ED
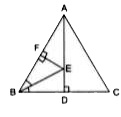
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB. Prove that :
(i) BD = CD
(ii) ED = EF
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
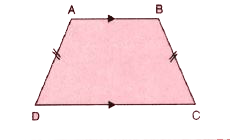
Diagonal AC= diagonal BD
View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC is perpendicular bisector of BD
View SolutionIn a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD
(ii) AC is perpendicular bisector of BD.
View SolutionABCD বৃত্তস্থ চতুর্ভূজের AB∣∣DC হলে প্রমাণ করো,AD=BC.
View Solution
