Determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at from their solubility product constants given in Table . Determine also the molarities of individual ions.
(i)Silver chromate ,
M, M
(ii) Barium chromate ,
M
M , M
(iii) Ferric hydroxide ,
M
M , M
(iv) Lead chloride ,
M
M
M
(v)Mercurous iodide ,
M
M
M .
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - EQUILIBRIUMEXERCISE - NCERT File ( Exemplar Problems MCQ-I)21videos
EQUILIBRIUM
- BOOK - MODERN PUBLICATIONCHAPTER - EQUILIBRIUMEXERCISE - NCERT File ( Exemplar Problems Short Answer Questions )16videos
EQUILIBRIUM
- BOOK - MODERN PUBLICATIONCHAPTER - EQUILIBRIUMEXERCISE - Problems (Advanced Level)17videos
EQUILIBRIUM
- BOOK - MODERN PUBLICATIONCHAPTER - ENVIRONMENTAL POLLUTION EXERCISE - UNIT PRACTICE TEST15videos
ENVIRONMENTAL POLLUTION
- BOOK - MODERN PUBLICATIONCHAPTER - HALOALKANES AND HALOARENESEXERCISE - UNIT PRACTICE TEST12videos
HALOALKANES AND HALOARENES
Similar Questions
Determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at 298 K form their solubility product constants given below. Determine also the molarities of individual ions.
KSP(Ag2CrO4)=1.1×10−12,
KSP(BaCrO4)=1.2×10−10,
KSP[Fe(OH)3]=1.0×10−38,
KSP(PbCI2)=1.6×10−5,
KSP(Hg2I2)=4.5×10−29.View SolutionDetermine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at 298 K form their solubility product constants given below. Determine also the molarities of individual ions.
KSP(Ag2CrO4)=1.1×10−12,
KSP(BaCrO4)=1.2×10−10,
KSP[Fe(OH)3]=1.0×10−38,
KSP(PbCI2)=1.6×10−5,
KSP(Hg2I2)=4.5×10−29.View Solution
Knowledge Check
- Question 1 - Select One
The standard reduction potential for two reactions are given below
AgCl(s)+e−→Ag(s)+Cl−(aq),E∘=0.22V
Ag+(aq)+e−→Ag(s),E∘=0.80V
The solubility product of AgCl under standard conditions of temperature is given byA1.6×10−5B1.5×10−8C3.2×10−10D1.5×10−10 - Question 2 - Select One
The process in which solution containing more than one typeof ions (either cation or anion) and in which one ion undergoes almst complete precipitation followed by the second ion and similarly second ion undergoes complete precipitation followed by the third ion is known as preferential precipitation. It is the solubility of the salt,not the solubility product of the salt, by means of which one can predict the preferential precipitation of the salt or ion among the lot of ions in the solution. For example , in a solution containing Cl−,Br− and I− ions, if Ag+ ions are added, then out of three , the less soluble salt is precipitated first . If the addition of Ag+ ions is continued, eventually , a stage is reached when the next lesser soluble salt starts precipitating along with the least soluble salt and so on.
If the stiochiometry of the salt is same, then the salt with the minimum Ksp ( solubility product ) will have minimum solubility and will precipitate first, followed by the salt of next higher solubility product and so on. If the stiochiometry of teh salt is not same, then from the solubility product data alone, we cannot predict which ions will precipitate first. For example, a solution containing Cl− and CrO2−4. In order to predict which ion will precipitate first, we have to calculate the amount of Ag+ ions needed to start precipitation through the solubility product data given. When AgNO93) is added to the solution, the minimum of the two concentrations needed to start the precipitation will be reached and thus corresponding [Ag+] to start the precipitation increases. Its concentration eventually becomes equal to the value required for CrO2−4 . At this stage, practically almost the whole of Cl− ions get precipitated . Addition of more AgNO3 causes simultaneous precipitation of both the ions together.
Suppose a student of chemistry performs the following two sets of experiments in order to known the preferential precipitation of ions as well as its precipitated percentage amount.
Experiment 1. He prepare a solution of anions composed of 0.1 M each of Cl−,Br− and I− . Further he adds gradually solid AgNO3 to this solution. He assumes that volume of the solution does not change after the addition of solid AgNO3(KspAgCl=1.0×10−9M2,KspAgBr=10−10M2 and KspAgI=10−12M2)
Experiment -2. He prepares a solution of cations Cd2+(0.2M) and Bi3+(0.3m) . Now he adds S2− ions into the solution of cations in order to separate them by selective precipitation Cd2+forms yellow precipitate of CdS and Bi3+ forms black precipitate of Bi2S3 with S2− ions respectively.
(KspBi2S3=9×10−25M5 and KspCdS=2×10−20M2).Answer the following questions ont he basis of the above write up.
Which of the following will precipitate first in experiment -1 ?AI−ionBBr− ionCCl− ionDcannot be predicted - Question 3 - Select One
The process in which solution containing more than one typeof ions (either cation or anion) and in which one ion undergoes almst complete precipitation followed by the second ion and similarly second ion undergoes complete precipitation followed by the third ion is known as preferential precipitation. It is the solubility of the salt,not the solubility product of the salt, by means of which one can predict the preferential precipitation of the salt or ion among the lot of ions in the solution. For example , in a solution containing Cl−,Br− and I− ions, if Ag+ ions are added, then out of three , the less soluble salt is precipitated first . If the addition of Ag+ ions is continued, eventually , a stage is reached when the next lesser soluble salt starts precipitating along with the least soluble salt and so on.
If the stiochiometry of the salt is same, then the salt with the minimum Ksp ( solubility product ) will have minimum solubility and will precipitate first, followed by the salt of next higher solubility product and so on. If the stiochiometry of teh salt is not same, then from the solubility product data alone, we cannot predict which ions will precipitate first. For example, a solution containing Cl− and CrO2−4. In order to predict which ion will precipitate first, we have to calculate the amount of Ag+ ions needed to start precipitation through the solubility product data given. When AgNO93) is added to the solution, the minimum of the two concentrations needed to start the precipitation will be reached and thus corresponding [Ag+] to start the precipitation increases. Its concentration eventually becomes equal to the value required for CrO2−4 . At this stage, practically almost the whole of Cl− ions get precipitated . Addition of more AgNO3 causes simultaneous precipitation of both the ions together.
Suppose a student of chemistry performs the following two sets of experiments in order to known the preferential precipitation of ions as well as its precipitated percentage amount.
Experiment 1. He prepare a solution of anions composed of 0.1 M each of Cl−,Br− and I− . Further he adds gradually solid AgNO3 to this solution. He assumes that volume of the solution does not change after the addition of solid AgNO3(KspAgCl=1.0×10−9M2,KspAgBr=10−10M2 and KspAgI=10−12M2)
Experiment -2. He prepares a solution of cations Cd2+(0.2M) and Bi3+(0.3m) . Now he adds S2− ions into the solution of cations in order to separate them by selective precipitation Cd2+forms yellow precipitate of CdS and Bi3+ forms black precipitate of Bi2S3 with S2− ions respectively.
(KspBi2S3=9×10−25M5 and KspCdS=2×10−20M2).Answer the following questions ont he basis of the above write up.
What percent of the anions Br− and I− get precipitated respectively when the third ion starts precipitating in experiment -1 ?A90%,99.9%B99.9%,90%C80%,90%D90%,80%
Determine the solubility of (a) AgCI, (b) Fe(OH)3, (c) Hg2Br2, and (d) Ag2SO4 from their solubility product constants give in table. Calculate the molarities of the individual ions and also the soubities of salts in gL−1.
View SolutionDetermine the solubility of silver chromate at 298 K given its Ksp value is 1.1×10−12?
View SolutionLead chloride has a solubility product of 1.7×10−5 at 298 K. Calculate its solubility at this temperature.
View Solution(a) Apply Kohlrausch law of independent migration of ions, write the expression to determine the limiting molar conductivity of calcium chloride.
(b) Given are the conductivity and molar conductivity of NaCI solutions at 298 K at different concentrations :
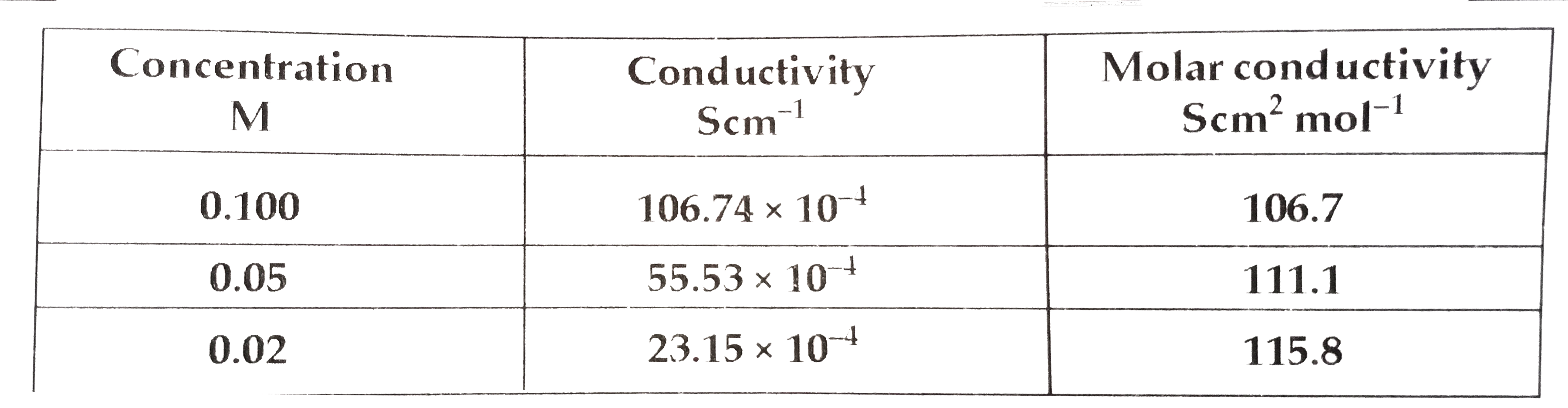
Compare the variation of conductivity and molar conductivity of NaCI solutions on dilution. Give reason.
(c) 0.1 M KCI solution offered a resistance of 100 ohms in conductivity cell at 298 K. If the cell constant of the cell is 1.29cm−1, calculate the molar conductivity of KCI solution.View SolutionCompreshension
The first demontration of the stereochmistry the SN2 reaction was carred out in 1935 by prof ,E,D Huges and his colleagues at the University of london , they allowed ® -2-iodooctane to react with readioactiver iodide ion .I−.
CH3CH∣I2- iodooctane(CH2)5CH3+⋅I−⇔CH3CH3∣^(⋅)2-iodooctaneradioactive (CH2_(5)Ch3+I−
the rate of subsittuiton (rate constantKs was determined by measuring the rate incoprotion of radioactvity into the alkyl halide the rate of loss of optical activity from the alky halide (rate constant K∘ was also deterined under the same coditions consitions . what ratio K∘/KS is prediected for each of hte following stereochemical scenarios :
For inversion reaction :
(A) K∘Ks=1 (b) K∘KS<1(c ) K∘Ks>1(d) can not be predicted
B. For equal amounts of both retention and inversion ?
K∘Ks=1 (b) (K_(@))/(K_(S))lt1(c)K_(@))/(K_(s))gt1(d) can not be predictedView Solution

