Let us look at the following triangular arragements of dots. First row has one dot,second row two dots and so on and throw will have n dots. Let L, be total number of dots in such a triangular arrangement of nrows of dots. Answer questions 16 and 17 below
Step by step video & image solution for Let us look at the following triangular arragements of dots. First row has one dot,second row two dots and so on and throw will have n dots. Let L, be total number of dots in such a triangular arrangement of nrows of dots. Answer questions 16 and 17 below by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
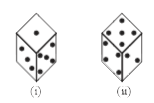
Three different positions of the same dice, which has one to six dots on its six faces, are shown below. When one dot is at the bottom the number of dots on the top will be:
 A5B2C4D3
A5B2C4D3Three different positions of the same dice, which has one to six dots on its six faces, are shown below. When six dots are at the bottom then the number of dots on the top will be :
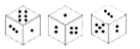 A5B3C2D4
A5B3C2D4
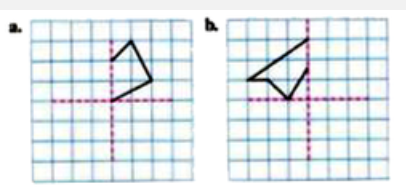
Complete the following figures so that the final figures has the two dotted lines as the two lines of symmetry.
 .
.
View SolutionRadha is drawing a dot Rangoli (a beautiful pattern of lines joining dots) with chalk powder. She has 9 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there if there are 8 rows? If there are 10 rows?
View SolutionRadha is drawing a dot Rangoli (a beautiful pattern of lines joining dots) with chalk powder. She has 9 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there if there are 8 rows? If there are 10 rows?
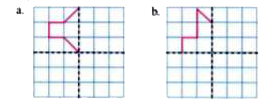
View SolutionComplete the figures below so that the final figure has the two dotted lines as the two lines of symmetry.
 .
.
View SolutionComplete the figures below so that the final figure has the two dotted lines as the two lines of symmetry.
 .
.
View SolutionComplete the figures below so that the final figure has the two dotted lines as the two lines of symmetry.
 .
.
View Solution