If the length of the perpendicular from the vertices of a triangle A,B,C on the opposite sides are $P_{1}, P_{2}, P_{3}$ then $\frac{1}{P_{1}} + \frac{1}{P_{2}} + \frac{1}{P_{3}} =$

Video Solution

|

Answer

Step by step video & image solution for If the length of the perpendicular from the vertices of a triangle A,B,C on the opposite sides are P_(1),P_(2),P_(3) then (1)/(P_(1))+(1)/(P_(2))+(1)/(P_(3))= by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One or More

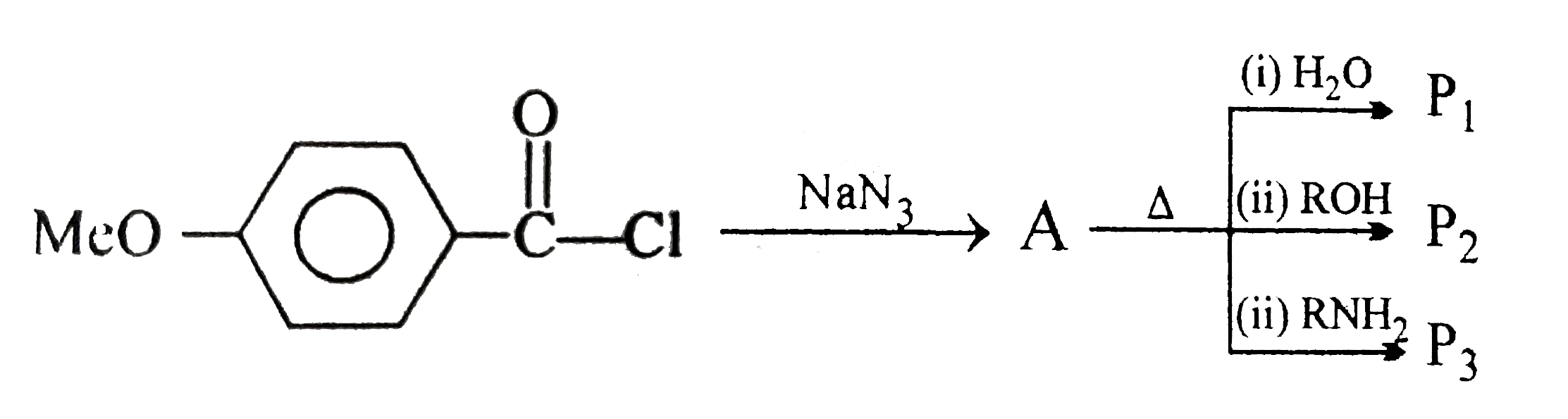
$P_{1}, P_{2}, P_{3}, a r e :$
A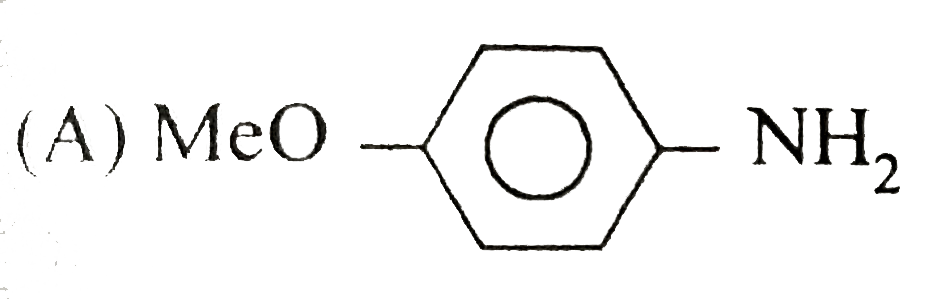
B
C
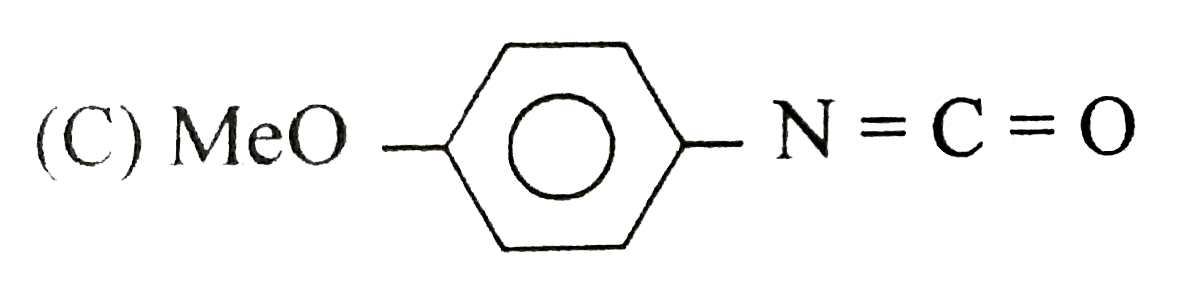D
Question 2 - Select One
If $p_{1}, p_{2}, p_{3}$ are respectively the perpendiculars from the vertices of a triangle to the opposite sides , then $\frac{cos A}{p_{1}} + \frac{cos B}{p_{2}} + \frac{cos C}{p_{3}}$ is equal to
A $1 / r$
B $1 / R$
C $1 /!$
Dnone of these
Question 3 - Select One
The length of the perpendicular drawn from any point in the interior of an equilateral triangle to the respective sides are $p_{1}, p_{2}$ and $p_{3}$ . The length of each side of the triangle is
A(a) $\frac{2}{\sqrt{3}} (p_{1} + p_{2} + p_{3})$
B(b) $\frac{1}{3} (p_{1} + p_{2} + p_{3})$
C(c) $\frac{1}{\sqrt{3}} (p_{1} + p_{2} + p_{3})$
D(d) $\frac{4}{\sqrt{3}} (p_{1} + p_{2} + p_{3})$

Recommended Questions

Home
Ask Doubt
Profile