Find the equivalent definition of f(x)=max.x2,(−x)2,2x(1−x)whre0≤x≤1
The correct Answer is:f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩(1−x)2,0≤x<1/32x(1−x),1/3≤x<2/3x2,2/3≤x≤1
Here, for maximum, let us consider f1(x)=x2,f2(x)=(1−x)2, and f3(x)=2x(1−x).
Now graph for f1(x),f2(x), and f3(x) are as follows.
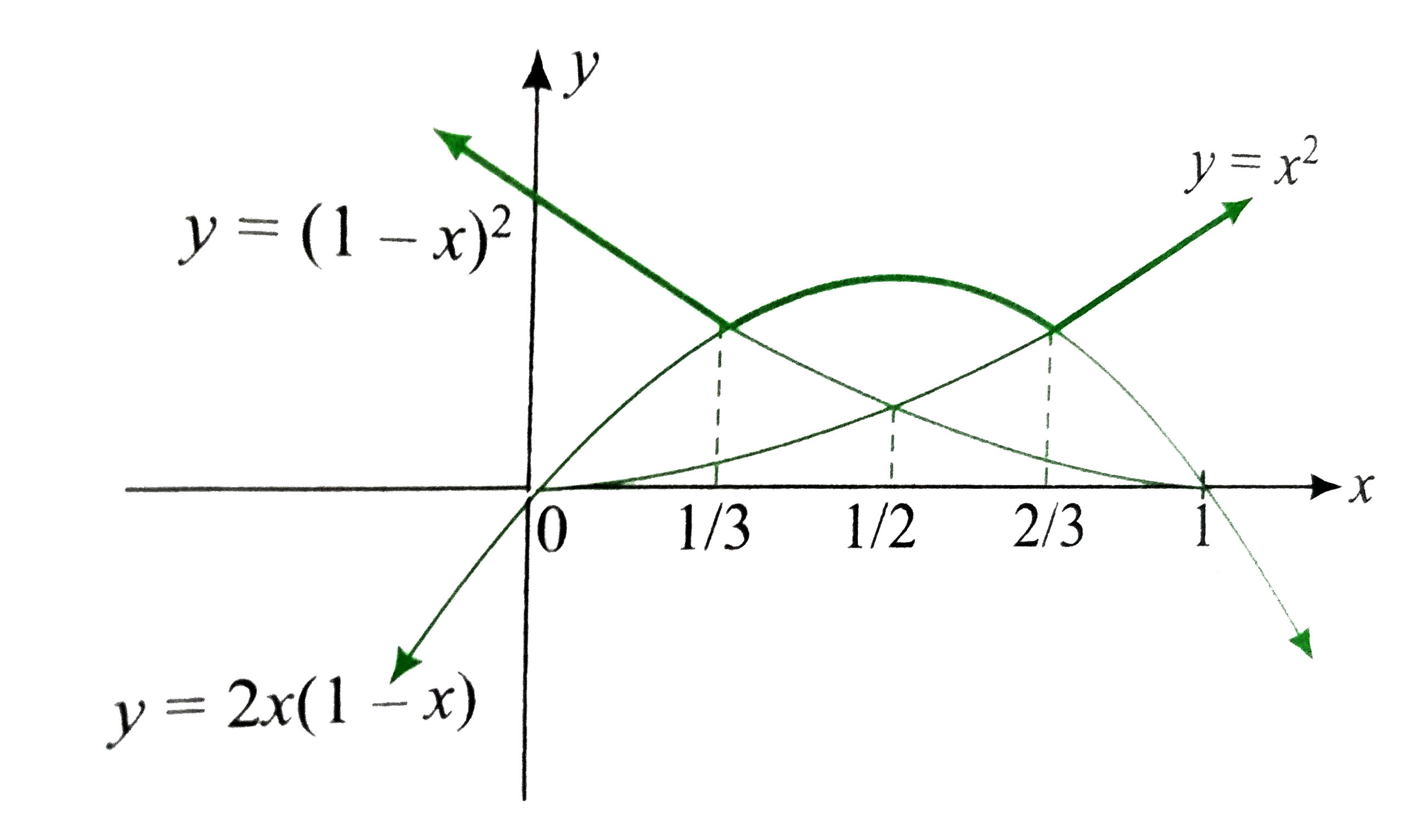
Here, neglect the graph that is below the points of intersection.
f(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩(1−x)2,0≤x<132x(1−x),13≤x<23x2,23≤x≤1
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.106videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.117videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.89videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank31videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the equivalent definition of the function. given by f(x) ={2xx≤00x<0
Af(x)=|x|Bf(x)=2xCf(x)=|x|+xDf(x)=2|x| - Question 2 - Select One
What is the equivalent definition of the function given by
f(x)={2x,x≥00,<0Af(x)=|x|Bf(x)=2xCf(x)=|x|+xDf(x)=2|x|
Find the derivative of f(x)={x−12x2−7x+5whenx≠1=13whenx=1atx=1.
View Solutionf(x)={4x<−1−4x−1≤x≤0 If f(x) is an even function in R then the definition of f(x) in (0,∞) is: (A) f(x)={4x0<x≤14x>1 (B) f(x)={4x0<x≤1−4x>1 (C) f(x)={40<x≤14xx>1 (D) f(x)={4x<−1−4x−1≤x≤0
View SolutionDiscuss the continuity of the function f(x) at x=1/2 , where f(x)={1/2−x; 0≤x<1/21; x=1/23/2−x; 1/2<x≤1
View SolutionFind k, if the following is p.d.f or r.v.f X.
f(x)={kx2(1−x)0<x<10otherwiseView SolutionFind the value of a+b if f(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪⎩ae1/|x+2|−12−e1/|x+2|;−3<x<−2b;x=−2sin(x4−16x5+32);−2<x<0 is continuous at x=−2.
View SolutionDiscuss the continuity of the function f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩x0≤x<121212x=121−x12<x≤1 at the point x=1/2 .
View Solution

