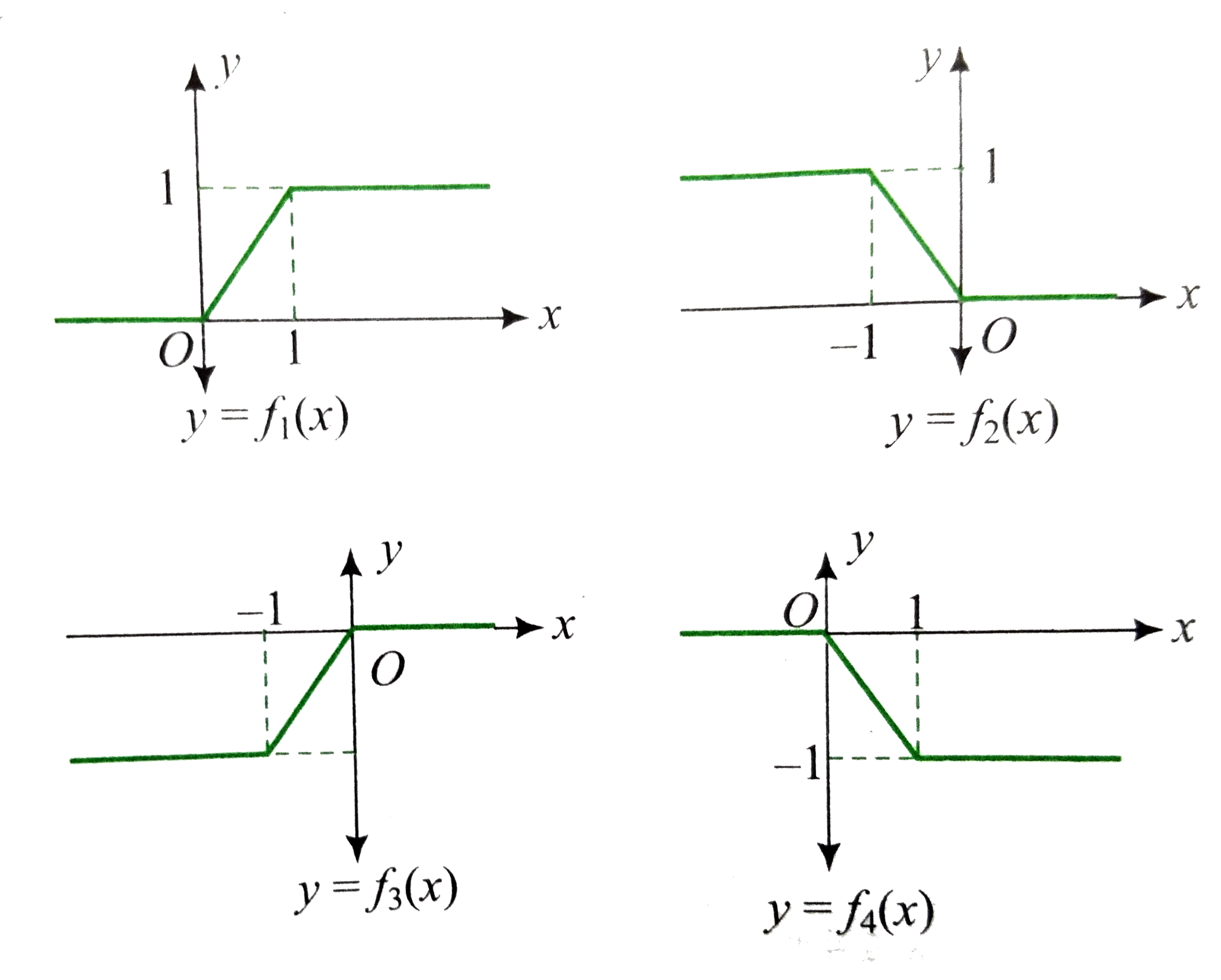
Let $f_{1} (x) = {x, x \leq x \leq 1 and 1 x > 1 and 0$ ,otherwise $f_{2} (x) = f_{1} (- x)$ for all x abd $f_{3} (x) = - f_{2} (x)$ for all x and $f_{4} (x) = - f_{3} (- x)$ for all x Which of the following is necessarily true?

A

$f_{4} (x) = f_{1} (x)$ for all x

B

$f_{1} (x) = - f_{3} (- x)$ for all x

C

$f_{2} (- x) = f_{4} (x)$ for all x

D

$f_{1} (x) + f_{3} (x) = 0$ for all x

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

|

Updated on:21/07/2023

Class 12 MATHS RELATIONS AND FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $f' (x) > f (x) for all x \geq 1 and f (1) = 0$ , then
A $e^{x} f (x)$ is a decreasing function
B $e^{- x} f (x)$ is an increasing function
C $f (x) > 0 for all x \in (1, \infty)$
D $f (x) < 0 for ll x \in [1, \infty)$
Question 2 - Select One
Let f(x) be defined for all $x > 0$ and be continuous. Let f(x) satisfy $f (x / y) = f (x) - f (y)$ for all x, y and $f (e) = 1$ . Then which of the following may be true
Af(x) is bounded
B $f (1 / x) \to 0$ as $x \to \infty +$
C $x f (x) \to 1$ as $x \to 0 +$
D $f' (x) = 1 / x$
Question 3 - Select One
If f(6-x)=f(x), for all x, then $\frac{1}{5} \int_{2}^{3} x [f (x) + f (x + 1)] d x$ is equal to :
A $\int_{3}^{4} f (x + 2) d x$
B $\int_{3}^{4} f (x + 1) d x$
C $\int_{1}^{2} f (x + 1) d x$
D $\int_{1}^{3} f (x) d x$

CENGAGE-RELATIONS AND FUNCTIONS-Exercise (Single)

Home
Ask Doubt
Profile