Match the following lists and then choose the correct code.

A
abcdprsq
B
abcdrsqp
C
abcdrqsp
D
abcdpqsr
Video Solution
Text Solution
The correct Answer is:B
a. f(x)=log3(5+4x−x2)
=log3(9−(x−2)2)
Now, −∞<9−(x−2)2≤9
But for f(x) to get defined, 0<9−(x−2)2≤9
or−∞<log3(9−(x−2)2)≤log39
or−∞<log3(9−(x−2)2)≤2
Hence, the range is (−∞,2].
b. f(x)=log3(x2−4x−5)
=log((x−2)2−9)
For f(x) to get defined, o<(x−2)2−9<∞
or limx→0logx<loge(x−2)2−9<limx→∞logx
or−∞<f(x)<∞
Hence, the range is R.
c. f(x)=log3(x2−4x+5)
=log3((x−2)2+1)
(x−2)2+1∈[1,∞)
or log3(x2−4x+5)∈[0,∞)
d. f(x)=log3(4x−5−x2)
=log3(−5−(x2−4x))
=log3(−1−(x−2)2)
Now, −1−(x−2)2<0 for all x.
Hence, the function is not defined.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Numerical)31videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - JEE Previous Year12videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)32videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank31videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the following lists and and then choose the correct code.

 AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
AabcdprqqBabcdqprsCabcdspqrDabcdrsqp - Question 2 - Select One
Match the following columns and then choose the correct option from amongst the given codes.
 A(p) (q) (r) (s)(1) (2) (4) (3)B(p) (q) (r) (s)(2) (1) (3) (4)C(p) (q) (r) (s)(3) (4) (2) (1)D(p) (q) (r) (s)(2) (1) (4) (3)
A(p) (q) (r) (s)(1) (2) (4) (3)B(p) (q) (r) (s)(2) (1) (3) (4)C(p) (q) (r) (s)(3) (4) (2) (1)D(p) (q) (r) (s)(2) (1) (4) (3) - Question 3 - Select One
Match the following column and choose the correct code
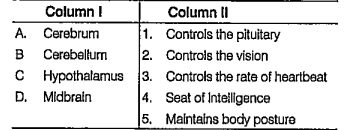 A
A B
B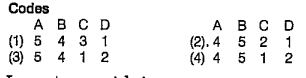 C
C D
D
Match the following columns and choose the correct code.
 View Solution
View SolutionMatch the following coloumns and choose the correct option from the codes given below
 View Solution
View SolutionMatch the following two lists and choose the correct answer from the codes given below:
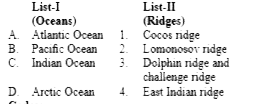 View Solution
View SolutionMatch the following two lists and choose the correct answer from the codes given below:
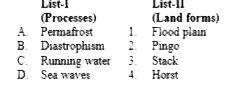 View Solution
View SolutionMatch the following columns and choose the correct option from codes given.
 View Solution
View Solution



