Suppose that f is an even, periodic function with period 2,andthatf(x)=x for all x in the interval [0,1] . The values of [10f(3.14)] is(where [.] represents the greatest integer function) ______
The correct Answer is:0.86
Since f is periodic with period 2 and f(x)=x∀x∈[0,1],andf(x) is even, there is symmetry about y-axis.
Therefore, graph of f(x) is as shown.
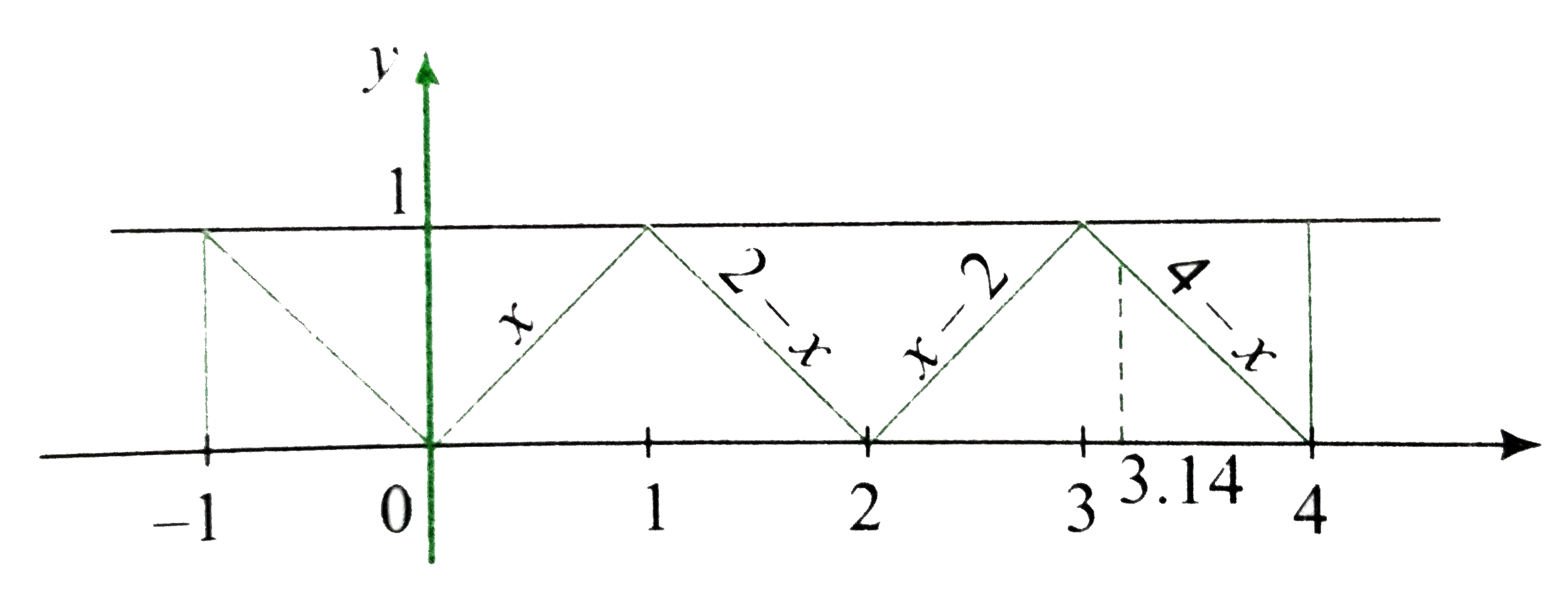
f(3.14)=4−3.14=0.86
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBook:CENGAGEChapter:RELATIONS AND FUNCTIONSExercise:JEE Previous Year
Explore 12 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGEChapter:RELATIONS AND FUNCTIONSExercise:Solved Examples And Exercises
Explore 498 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGEChapter:RELATIONS AND FUNCTIONSExercise:Exercise (Matrix)
Explore 9 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBook:CENGAGEChapter:Quadratic Equations, Inequalities, Modulus and LogarithmsExercise:Question Bank
Explore 31 Videos
- SCALER TRIPLE PRODUCTS Book:CENGAGEChapter:SCALER TRIPLE PRODUCTS Exercise:DPP 2.3
Explore 11 Videos
Similar Questions
Suppose that f is an even, periodic function with period 2,andthatf(x)=x for all x in the interval [0,1] . The values of [10f(3.14)] is(where [.] represents the greatest integer function) ______
View SolutionSuppose that f is even, periodic function with period 2, and that f(x) = x for all x in the interval [0, 1]. Then draw the graph of y = f(x).
View Solution
Knowledge Check
If f(x)=|x−1|.([x]=[−x]), then (where [.] represents greatest integer function)
Af(a) is continuous and differentiable at x = 1Bf(x) is discontinuous at x = 1Cf(x) is continuous at x = 2Df(x) is continuous but non-differentiable at x= 1The domain of the function f(x)=1√[x]2−[x]−20 is (where, [.] represents the greatest integer function)
A(−∞,−4)∪[6,∞)B(−∞,4]∪[6,∞)C(−∞,4)∪(6,∞)DNone of these
The period of 6x−[6x] is (where [ ] denotes the greatest integer function)
View SolutionFind the range of f(x)=x−[x]1−[x]+x',where[] represents the greatest integer function.
View Solutionf:(2,3)−−→0,1def∈edbyf(x)=x−[x],where[.] represents the greatest integer function.
View SolutionFind the domain of the function f(x)=1[x]2−7[x]−8, where [.] represents the greatest integer function.
View SolutionLet [.] represent the greatest integer function and f(x)=[tan2x] then :
View SolutionDiscuss the differentiability of f(x)=[x]+|1−x|,x∈(−1,3),where[.] represents greatest integer function.
View Solution