Match the following lists :

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

a. $Area = 2 (\frac{1}{2} 1 \times 1) = 1$ sq. units.

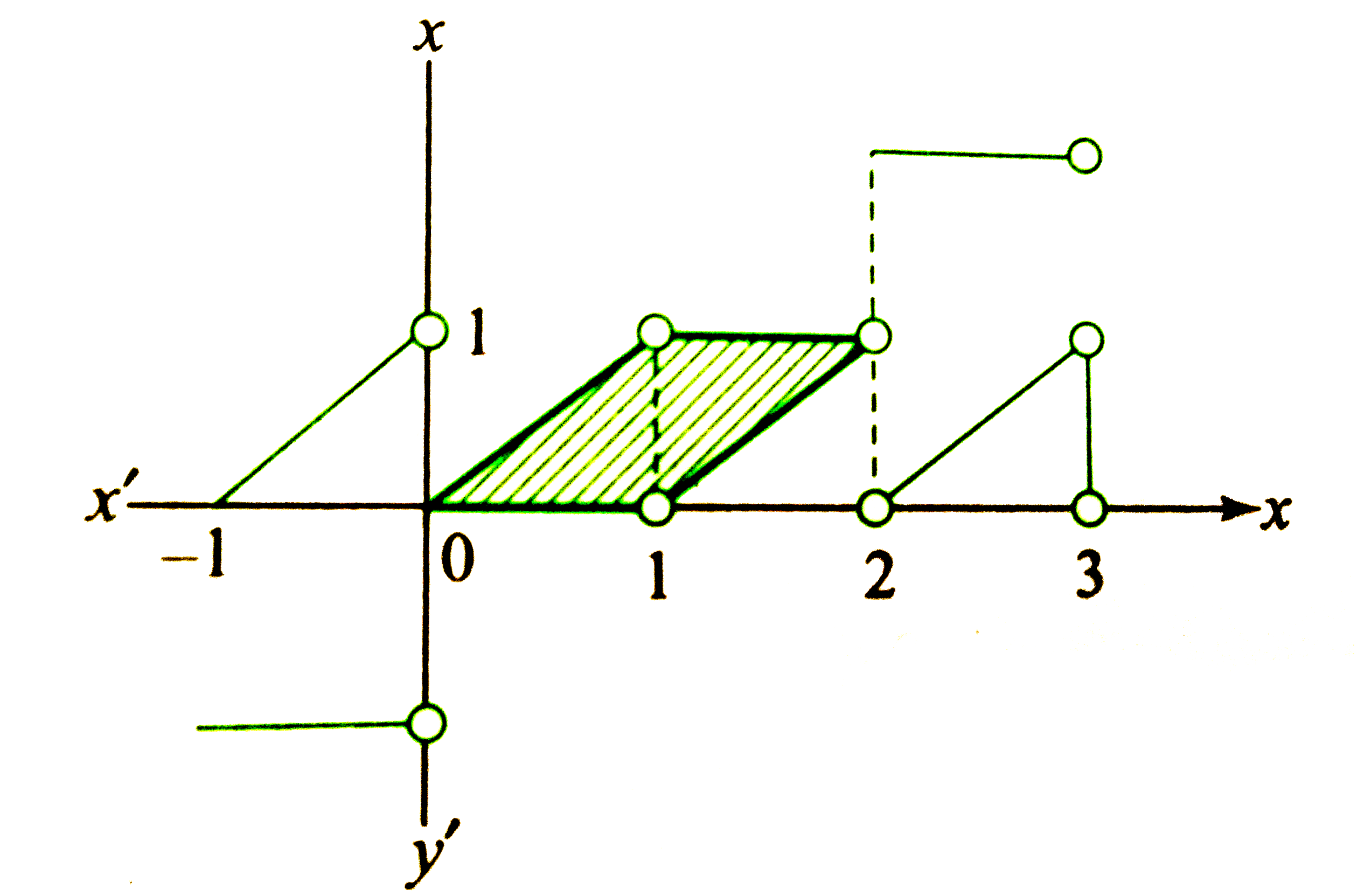
b. $y^{2} = x^{3} and | y | = 2 x,$ both the curve are symmetric about y-axis

$4 x^{2} = x^{3} or x = 0, 4 .$
$Required area = 2 4 \int 0 (2 x - x^{3 / 2}) d x = \frac{32}{5}$ sq. units.
c. $\sqrt{x} + \sqrt{| y |} = 1$

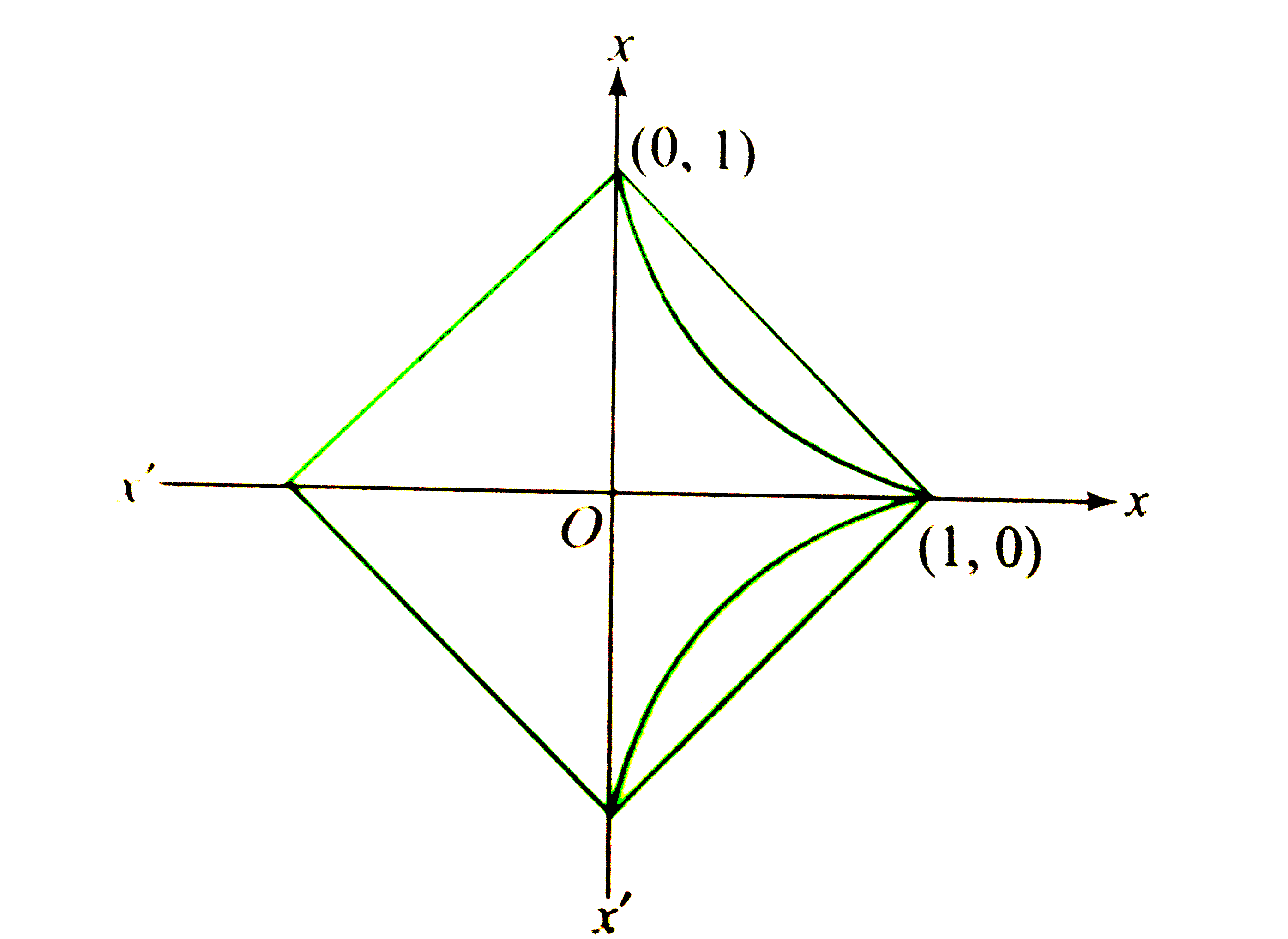
The curve is symmetrical about x-axis
$\sqrt{| y |} = 1 - \sqrt{x} and \sqrt{x} = 1 - \sqrt{| y |}$
$\Rightarrow for x > 0, y > 0 \sqrt{y} = 1 - \sqrt{x}$
$\frac{1}{2 \sqrt{y}} \frac{d y}{d x} = - \frac{1}{2 \sqrt{x}}$
$\frac{d y}{d x} = - \sqrt{\frac{y}{x}}$
$\frac{d y}{d x} < 0, function is decreasing$
$Required area = 2 1 \int 0 ((1 - x) - (1 - 2 \sqrt{x} + x)) d x$
$= 4 1 \int 0 (\sqrt{x} - x) d x$
$= 4 {[\frac{x^{3 / 2}}{3 / 2} - \frac{x^{2}}{2}]}_{0}^{1}$
$= 4 [\frac{2}{3} - \frac{1}{2}]$
$= \frac{2}{3}$ sq. units.
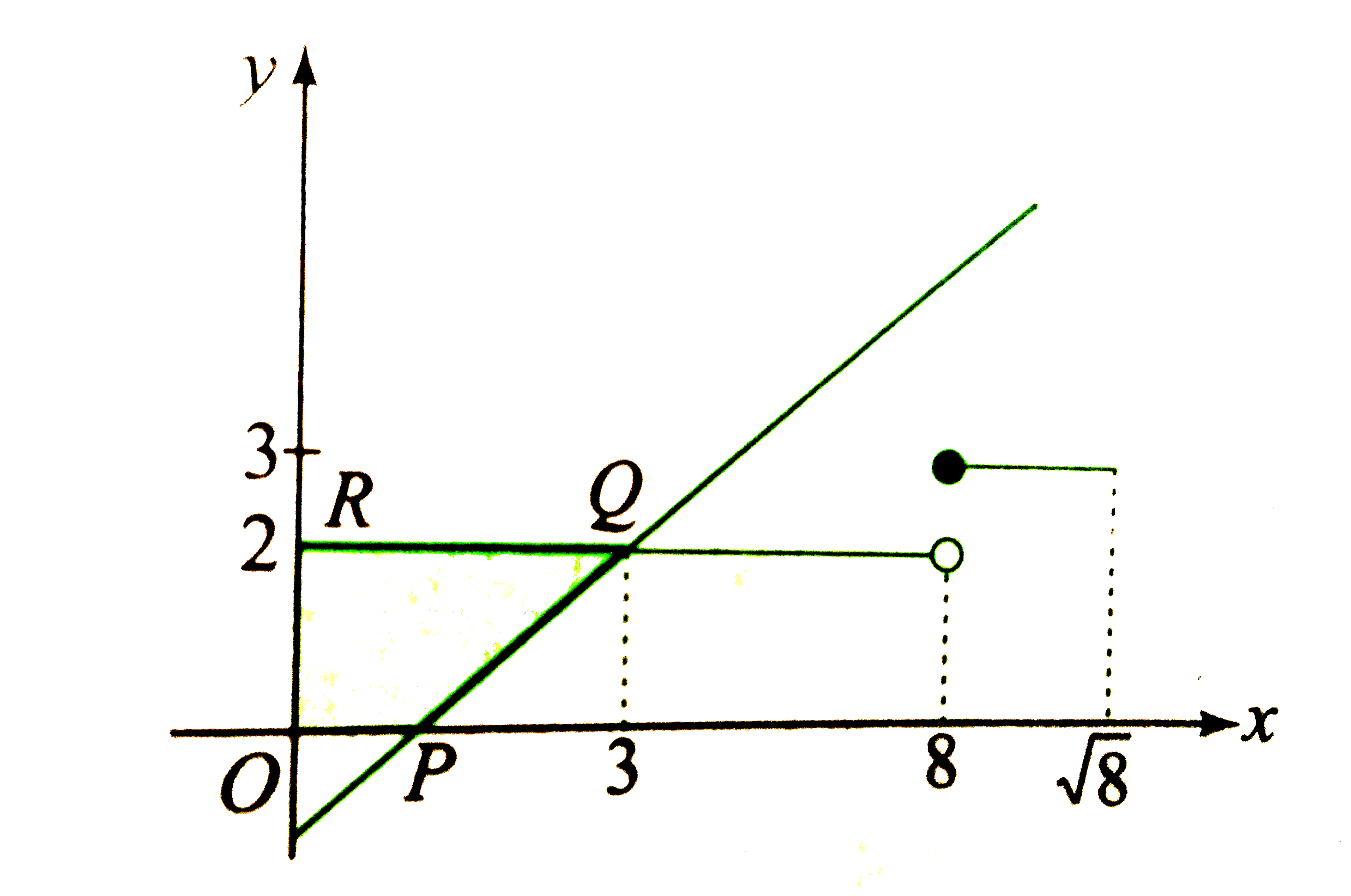
d. If $- 8 < x < 8,$ then y=2.
$If x \in (- 8 \sqrt{2}, - 8] \cup [8, 8 \sqrt{2}), then y = 3,$ and so on
Intersection of $y = x - 1 and y = 2 . We get x = 3 \in (- 8, 8) .$
Intersection of $y = x - 1 and y = 3$ .
$We get x = 4 \notin (- 8 \sqrt{2}, - 8] \cup [8, 8 \sqrt{2})$ .
$Similarly, y = x - 1 will not intersect y = [\frac{x^{2}}{64} + 2] at any$
other integral, except in the interval $x \in (- 8, 8) .$
Required area (shaded region ) $= 2 \times 3 - \frac{1}{2} \times 2 \times 2$
=4 sq. units.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

CENGAGE-AREA-Exercise (Matrix)

Home
Ask Doubt
Profile