The area (in sq units) of the region bounded by the curve and the lines is
A
B
C
D
Video Solution
Text Solution
The correct Answer is:A
is the region of first quadrant and fourth quadrant.
is half the region of the plane divided by the line
where origin lies.
is the region inside the parabola
is the region inside the parabola which has vertex at (0,1).
So, the required region is as shown in the following figure.
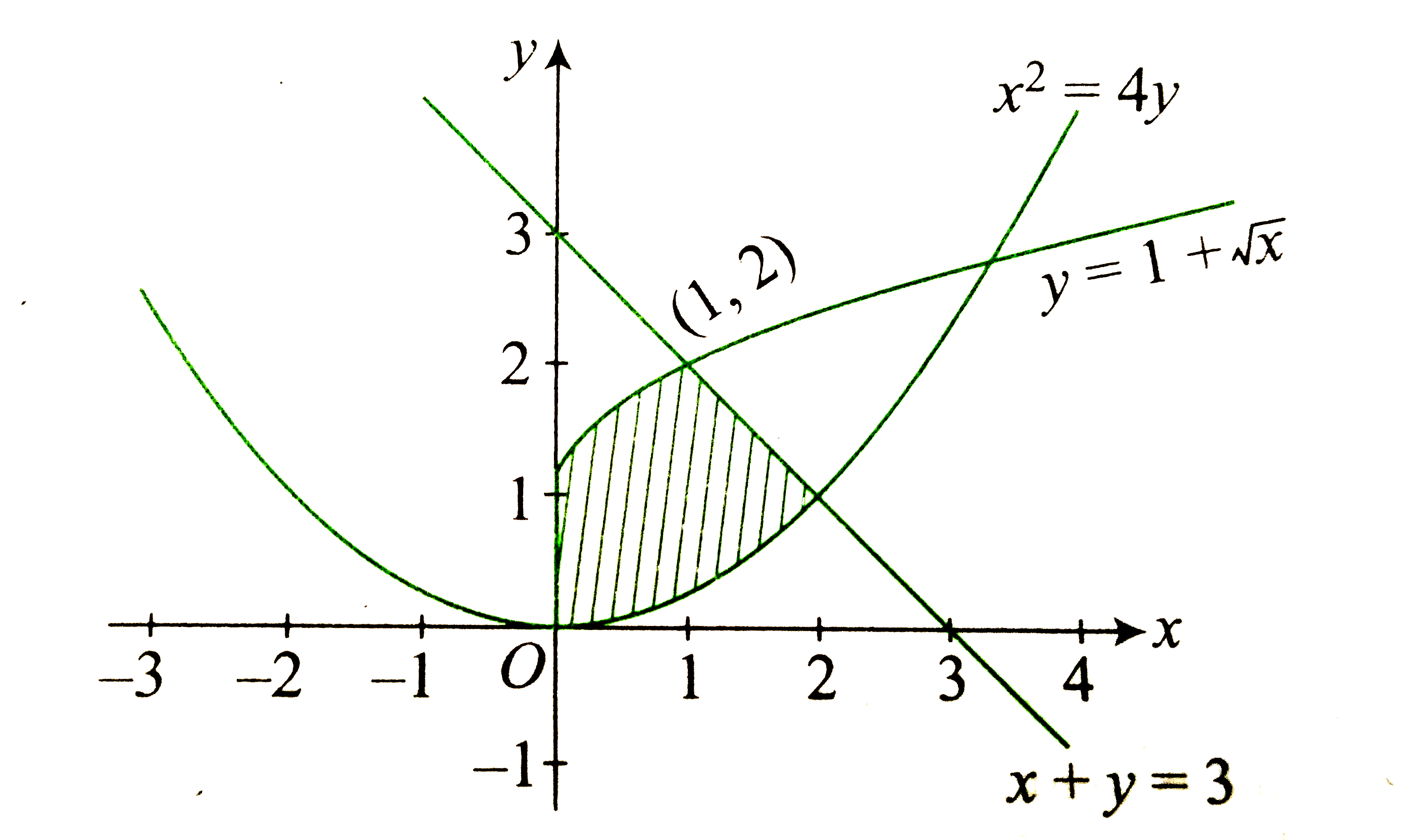
From the figure,
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Multiple Correct Answer Type
3 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)
16 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
The area (in sq units) of the region bounded by the curve 2x=y2−1andx=0 is
A1/3B2/3C1D2Area of the region bounded by the curve y=tanx and lines y = 0 and x = 1 is
A∫10and(1−x)dxBtan1−∫tan10tan−1ydyC∫tan10tan−1ydyD∫10tan−1xdxArea (in square units) of the region bounded by the curve y2=4x,y-axis and the line y=3 , is
A2B9/4C6√3Dnone of these
Area of the region bounded by the curves y=4,y=√x and x=−√y is
View SolutionThe area of the region bounded by the curve y=x2 and the line y=16 is :
View SolutionThe area (in sq unit) of the region enclosed by the curves y=x2andy=x3 is
View SolutionThe area of the region bouned by the curve y=2x−x2 and the line y=x is
View SolutionThe area (in sq units) of the region bounded by the curves y=ex, y=loge x and lines x = 1, x = 2 is
View Solution
