The incentre of a triangle with vertices (7,1),(−1,5) and (3+2√3,3+4√3) is
A
(3+2√3,3+4√3)
B
(1+23√3,1+43√3)
C
(7,1)
D
None of these
Video Solution
Text Solution
The correct Answer is:A
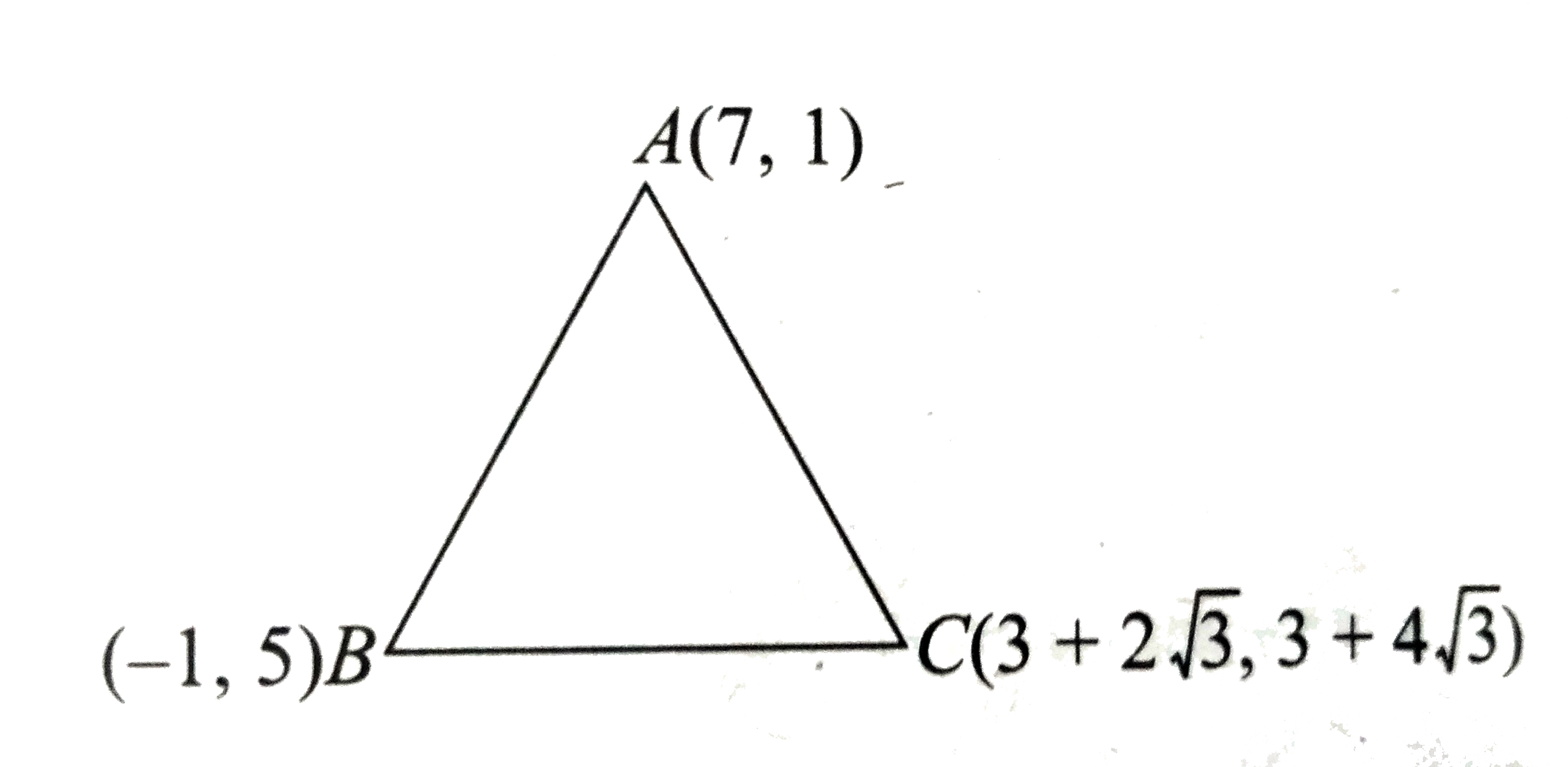
∵AB=BC=CA=4√5
i.e., given triangle is equilateral.
Hence, incentre =(7−1+3+2√33,1+5+3+4√33) (centroid) =(3+2√3,3+4√3)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Comprehension Type4videos
COORDINATE SYSTEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Question Bank22videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main Previous Year6videos
COORDINATE SYSYEM
Similar Questions
Knowledge Check
- Question 1 - Select One
The triangle with vertices (2,4), (2,6) and (2+√3 ,5) is
Aisosceles and right- angledBalways isoscelesCright- angledDequilateral - Question 2 - Select One
The incentre of triangle with vertices (1,√3),(0,0) and (2, 0) is
A(1,√32)B(23,1√3)C(23,√32)D(1,1√3)
The incetre of the triangle with vertices (1,√3),(0,0) and (2,0) is
View SolutionThe incentre of triangle with vertices (1,√3),(0,0) and (2, 0) is
View SolutionInradius of the triangle with vertices (1,1), (-1,-1), (−√3,√3) is
View SolutionFind the incentre of the triangle with vertices (1,√3),(0,0) and (2,0)
View SolutionThe incenter of the triangle with vertices (1,√3),(0,0), and (2,0) is (a)(1,√32) (b) (23,1√3) (c)(23,√32) (d) (1,1√3)
View Solution14√3−3√5
View Solution

