Let P be the point (−3,0) and Q be a moving point (0,3t). Let PQ be trisected at R so that R is nearer to Q. RN is drawn perpendicular to PQ meeting the x-axis at N. The locus of the mid-point of RN is
(x+3)2−3y=0
(y+3)2−3x=0
x2−y=1
y2−x=1
The correct Answer is:D
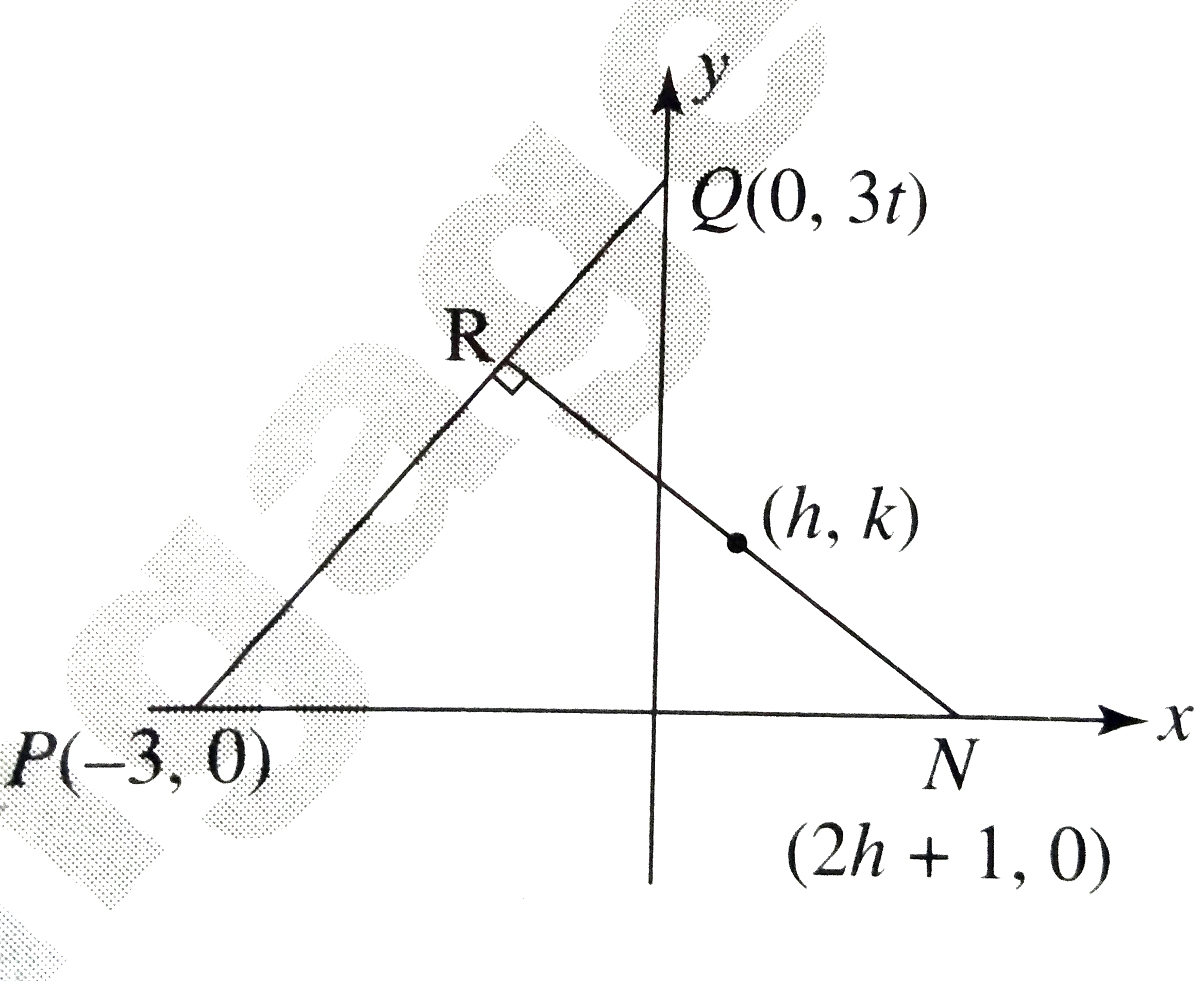
P(−3,0),Q(0,3t),R(−1,2t)
Let the mid point of RN be (h,k)
∴k=t.
RN⊥PQ⇒2t−2h−2×3t3=−1
⇒2t2=2h+2
⇒t2=h+1
⇒k2=h+1
Topper's Solved these Questions
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Comprehension Type
4 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Question Bank
22 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main Previous Year
6 Videos
Similar Questions
Let A be a fixed point (0,6) and B be a moving point (2t,0). Let M be the mid-point of AB and the perpendicular bisector of AB meets the y-axis at C. The locus of the mid-point P of MC is :
View Solutionlet P be the point (1,0) and Q be a point on the locus y2=8x. The locus of the midpoint of PQ is
View Solution
Knowledge Check
Q is any point on the circle x2+y2=9.QN is perpendicular from Q to the x-axis. Locus of the point of trisection of QN is
A4x2+9y2=36B9x2+4y2=36C9x2+y2=9Dx2+9y2=9Let P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
AP1 lies on C2andQ1 lies on C1BPQ≥min{PP1,QQ1}Cpoint P0 on C1 such that P0Q0≤PQ for all pairs of points (P,Q) is (13,109)Dpoint Q0 on C2 such that P0Q0≤PQ for all pairs of points (P,Q) is (109,13)Let P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
Ax2+4y+2=0Bx2−4y+6=0Cy2−4x+2=0Dy2+4x+2=0
Let A3(0,4)andBs(21,0)∈R. Let the perpendicular bisector of AB at M meet the y-axis at R. Then the locus of midpoint P of MR is y=x2+21
View SolutionThe tangent at any point P on y2=4x meets x-axis at Q, then locus of mid point of PQ will be
View SolutionLet coordinates of the points A and B are (5, 0 ) and (0, 7) respectively. P and Q are the variable points lying on the x- and y-axis respectively so that PQ is always perpendicular to the line AB. Then locus of the point of intersection of BP and AQ is
View SolutionA variable tangent to the parabola y2=4ax meets the parabola y2=−4ax P and Q. The locus of the mid-point of PQ, is
View SolutionLet P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
View Solution
