Question

If $A(3,4)$ and $B(-5,-2)$ are the extremities of the base of an isosceles triangle ABC with tan $C=2$, then point C can be

Options

A. `((3sqrt(5)-1)/(2),-(1+2sqrt(5)))`
B. `(-((3sqrt(5)+5))/(2),3+2sqrt(5))`
C. `((3sqrt(5)-1)/(2),3-2sqrt(5))`
D. `(-((3sqrt(5)-5))/(2),-(1-2sqrt(5)))`

Answer

A::B

Explanation

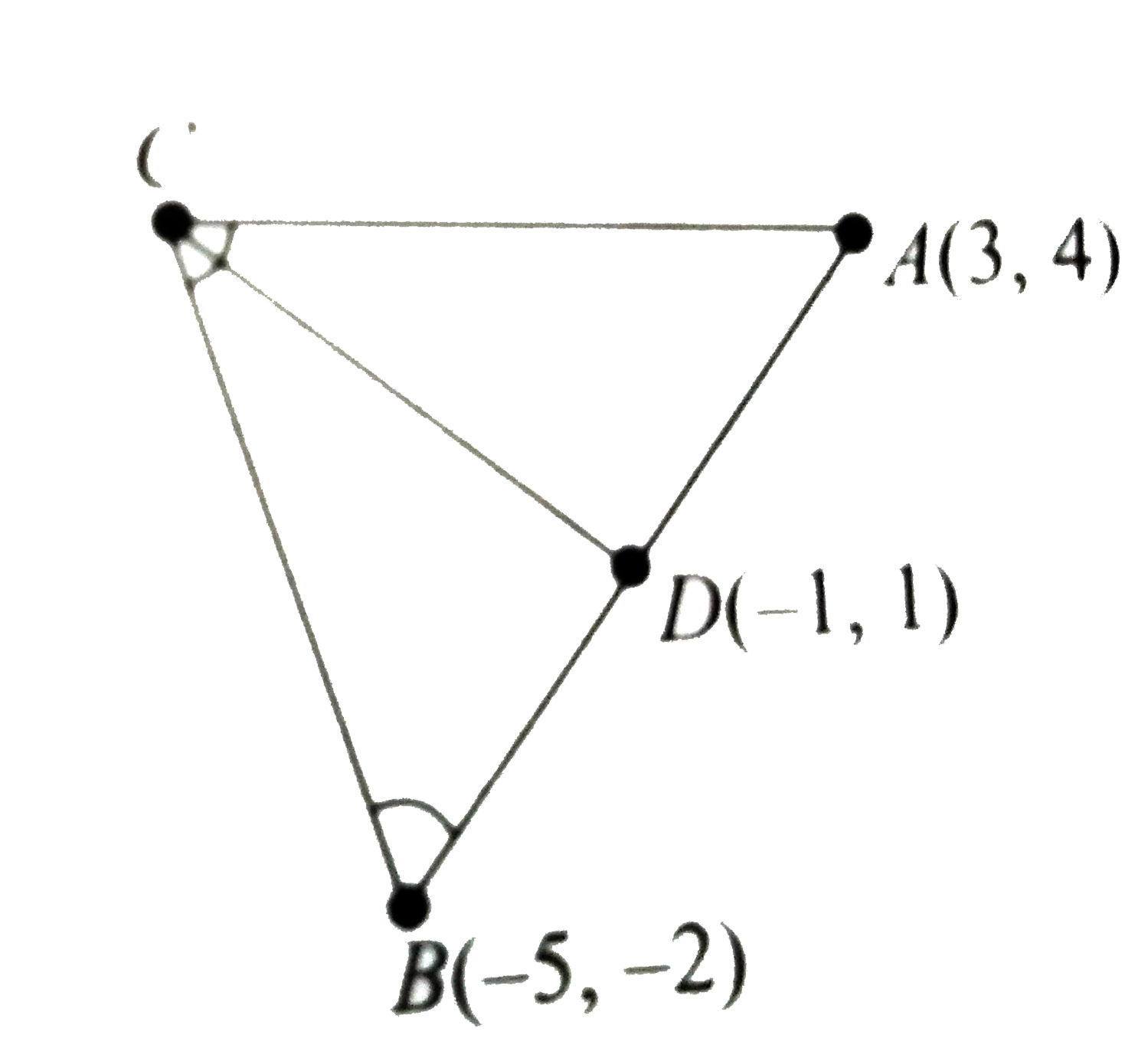
`D(-1,1)` is midpoint of AB.
`CD = BD cot.(C)/(2) =5. cot.(C)/(2)`
Now, `tan C = 2`
`rArr (2tan.(C)/(2))/(1-tan^(-2).(C)/(2)) =2`
`rArr tan^(2).(C)/(2) +tan.(C)/(2)-1 =0`
`rArr tan.(C)/(2) =(-1+sqrt(5))/(2)`
`rArr cot.(C)/(2) =(sqrt(5)+1)/(2)`
`rArr CD = 5 ((sqrt(5)+1)/(2)) =(5)/(2) (sqrt(5)+1)`
Slope of BD is `3//4`.
`:.` Slope of CD is `-4//3 = tan alpha`
Using parametric form of straight line, coordinates of C are given by
`(-1+-(5(sqrt(5)+1))/(2)cos alpha,1+-(5(sqrt(5)+1))/(2)sin alpha)`
or `(-(5+3sqrt(5))/(2),2sqrt(5)+3)` and `((3sqrt(5)-1)/(2),-(2sqrt(5)+1))`