Let C be the circle of radius unity centred at the origin. If two positive numbers $x_{1} and x_{2}$ are such that the line passing through $(x_{1}, - 1) and (x_{2}, 1)$ is tangent to C then $x_{1} \cdot x_{2}$

A

$x_{1} x_{2} = 1$

B

$x_{1} x_{2} = - 1$

C

$x_{1} + x_{2} = 1$

D

$4 x_{1} x_{2} = 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

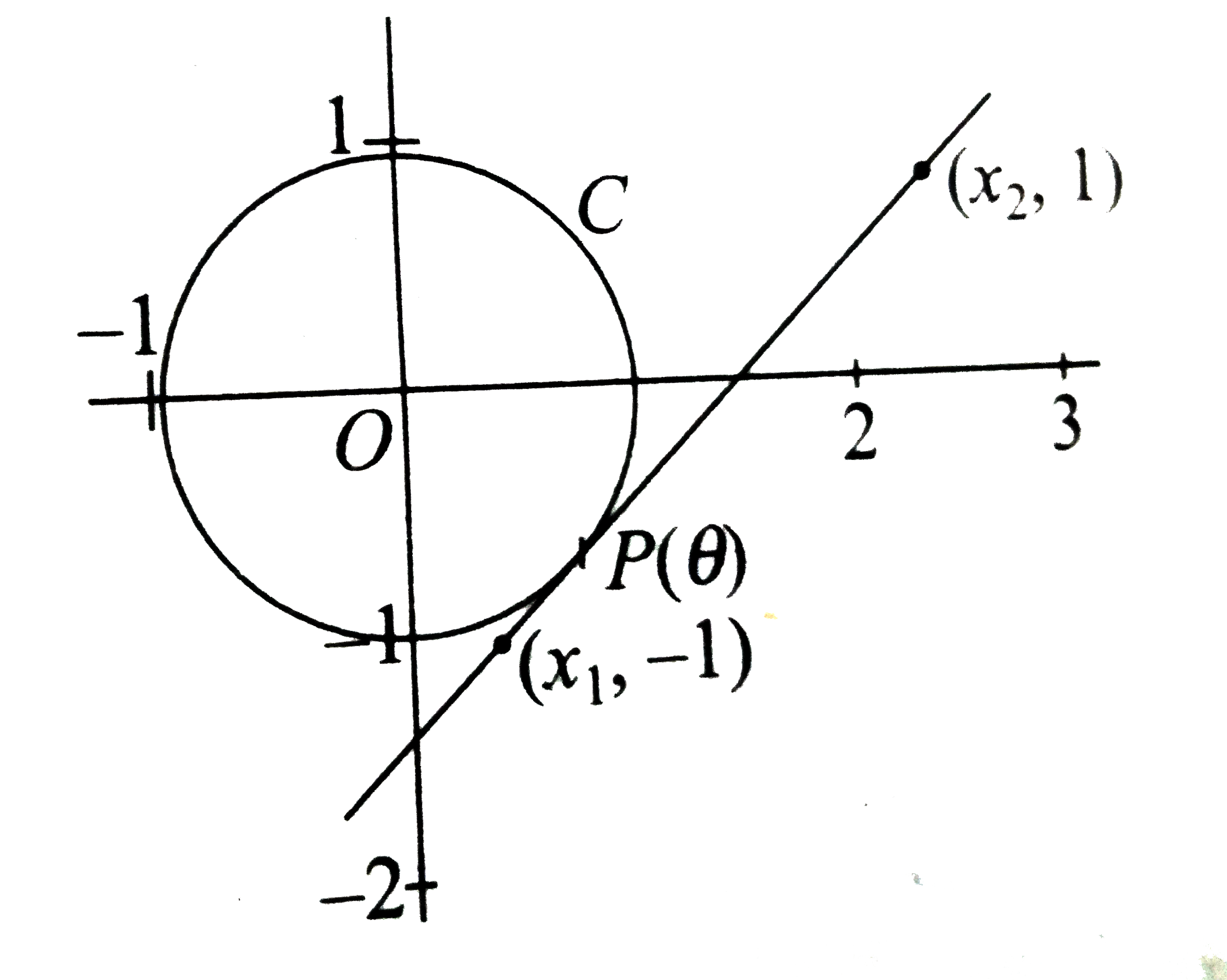
Equation of circle is $x^{2} + y^{2} = 1$
The equation of tangent to circle at any point $(cos θ, sin θ)$ is $x cos θ + y sin θ = 1$ .
Since it is passing through points $(x_{1}, - 1)$ and $(x_{2}, 1)$ we have
$x_{1} cos θ - sin θ = 1$ or $x_{1} cos θ = 1 + sin θ$ (i)
and $x_{2} cos θ = 1 - sin θ$ (ii)
Multiplying the results, we have
$x_{1} x_{2} {cos}^{2} θ = 1 - {sin}^{2} θ$
$\Rightarrow x_{1} x_{2} {cos}^{2} θ = {cos}^{2} θ$
$\Rightarrow x_{1} x_{2} = 1$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Equation of the circle , centred at the origin , whose radius equals the distance between the lines x = -1 and x = 1 , is
A $x^{2} + y^{2} = 1$
B $x^{2} + y^{2} = 2$
C $x^{2} + y^{2} = 4$
D $x^{2} + y^{2} = - 4$
Question 2 - Select One
A circle passes through a fixed point A and cuts two perpendicular straight lines through A in B and C. If the straight line BC passes through a fixed-point $(x_{1}, y_{1})$ , the locus of the centre of the circle, is
A $\frac{x_{1}}{x} + \frac{y_{1}}{y} = 1$
B $x_{1} y = x_{1} y_{1}$
C $x y_{1} + y x_{1} = 2$
D $\frac{x_{1}}{x} + \frac{y_{1}}{y} = 2$
Question 3 - Select One
Joint equation of lines passing through the origin, and parallel to the lines $y - m_{1} x + c_{1}$ and $y = m_{1} x + c_{2}$ , is
A $m_{1} m_{2} x^{2} - (m_{1}_m_{2}) x y + y^{2} = 0$
B $m_{1} m_{2} x^{2} + (m_{1} + m_{2}) x y + y^{2} = 0$
C $m_{1} m_{2} y^{2} - (m_{1} + m_{2}) x y + x^{2} = 0$
D $m_{1} m_{2} y^{2} + (m_{1} + m_{2}) x y + x^{2} = 0$

CENGAGE-CIRCLES-Single Correct Answer Type

Home
Ask Doubt
Profile